线性回归
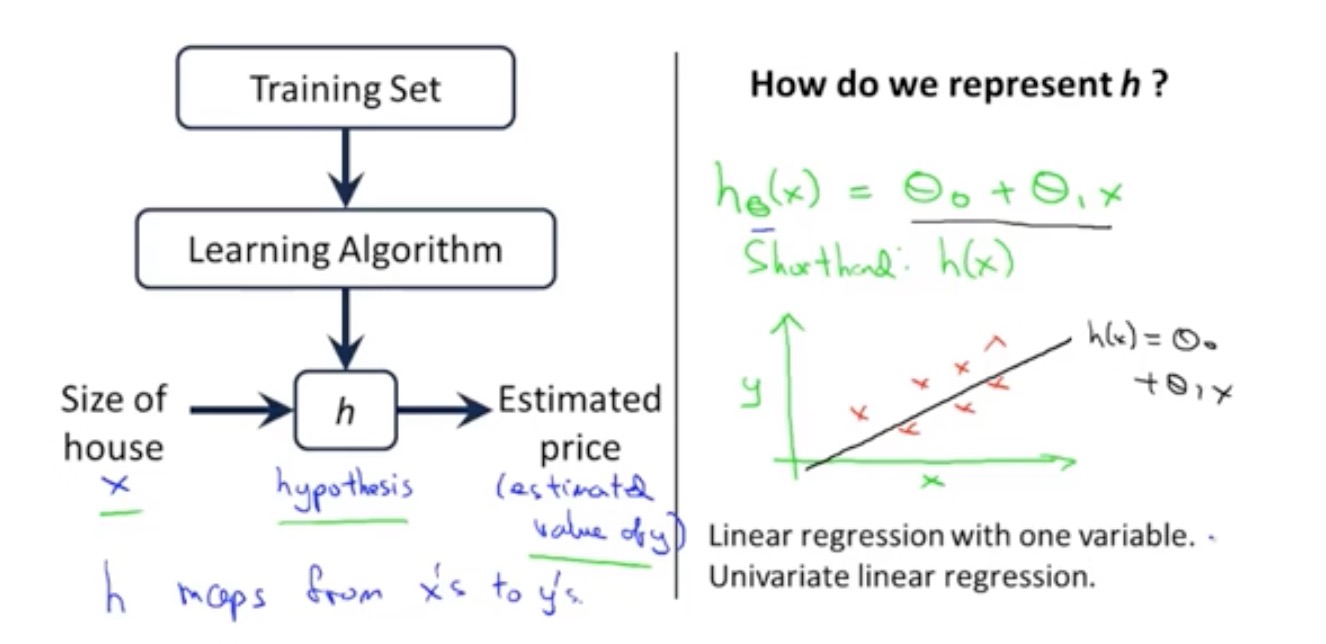
模型描述
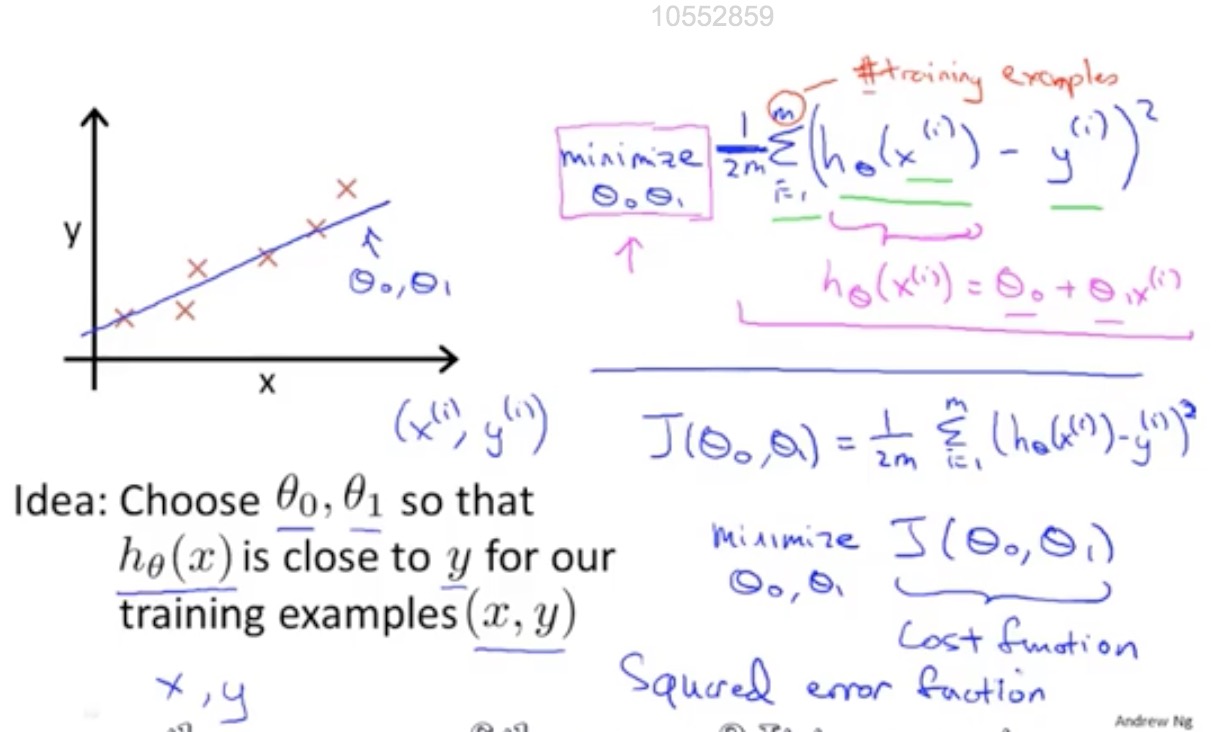
代价(损失)函数
平方误差

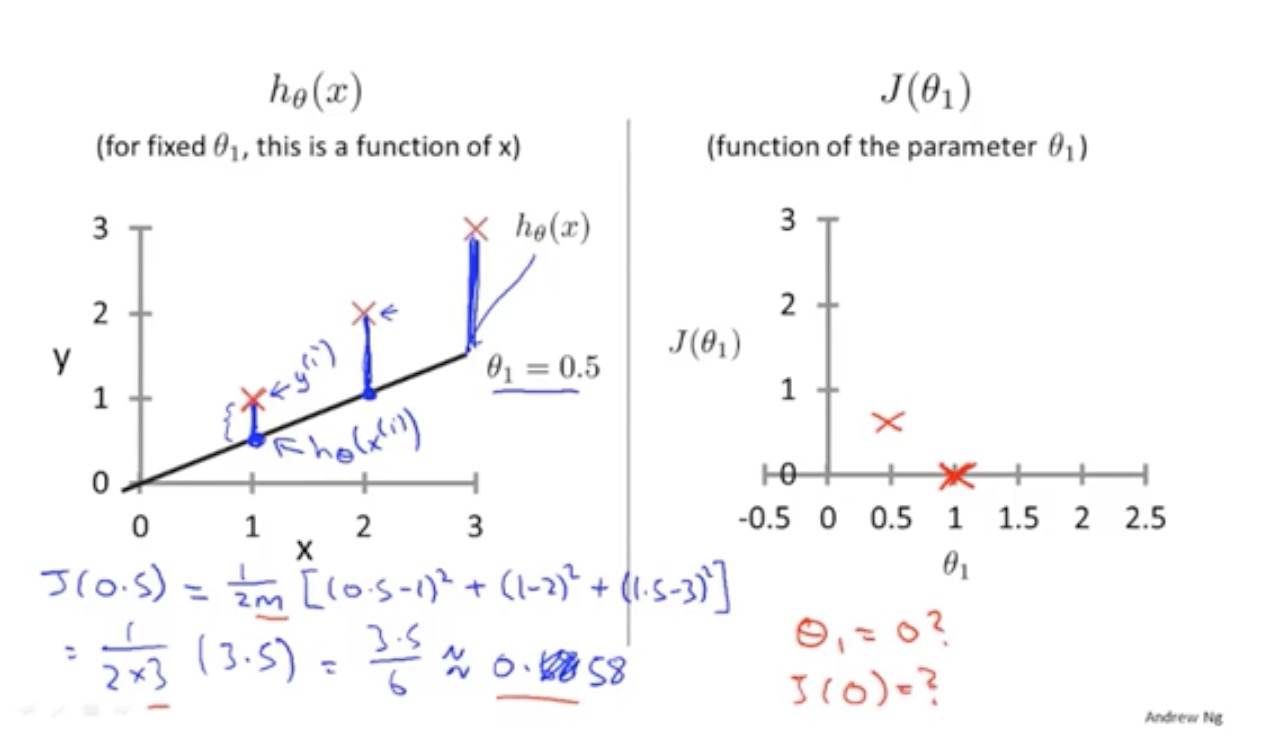

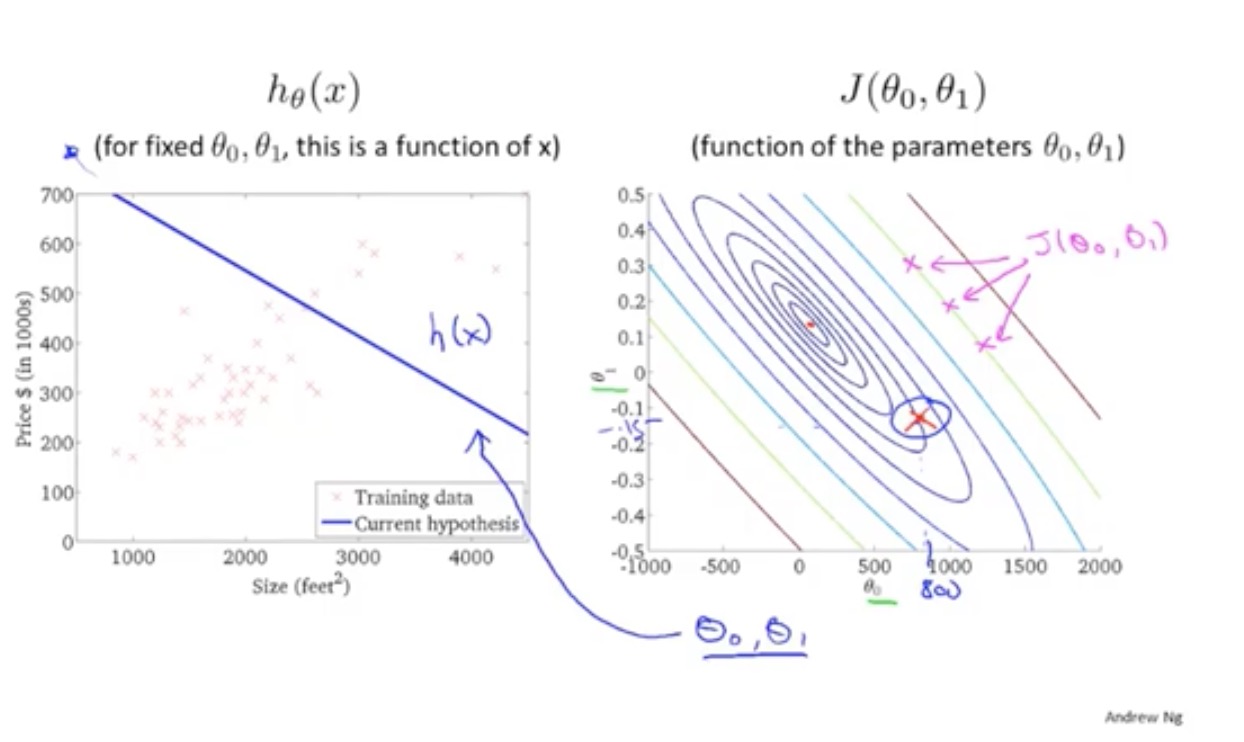
三维模型图


梯度下降
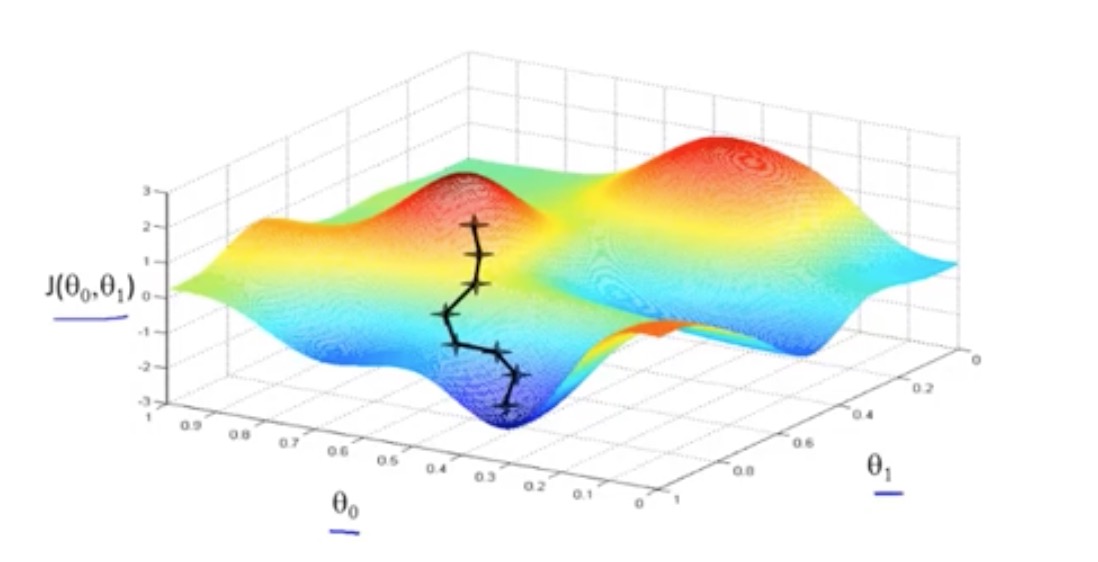
同步更新


线的斜率,导数项为0
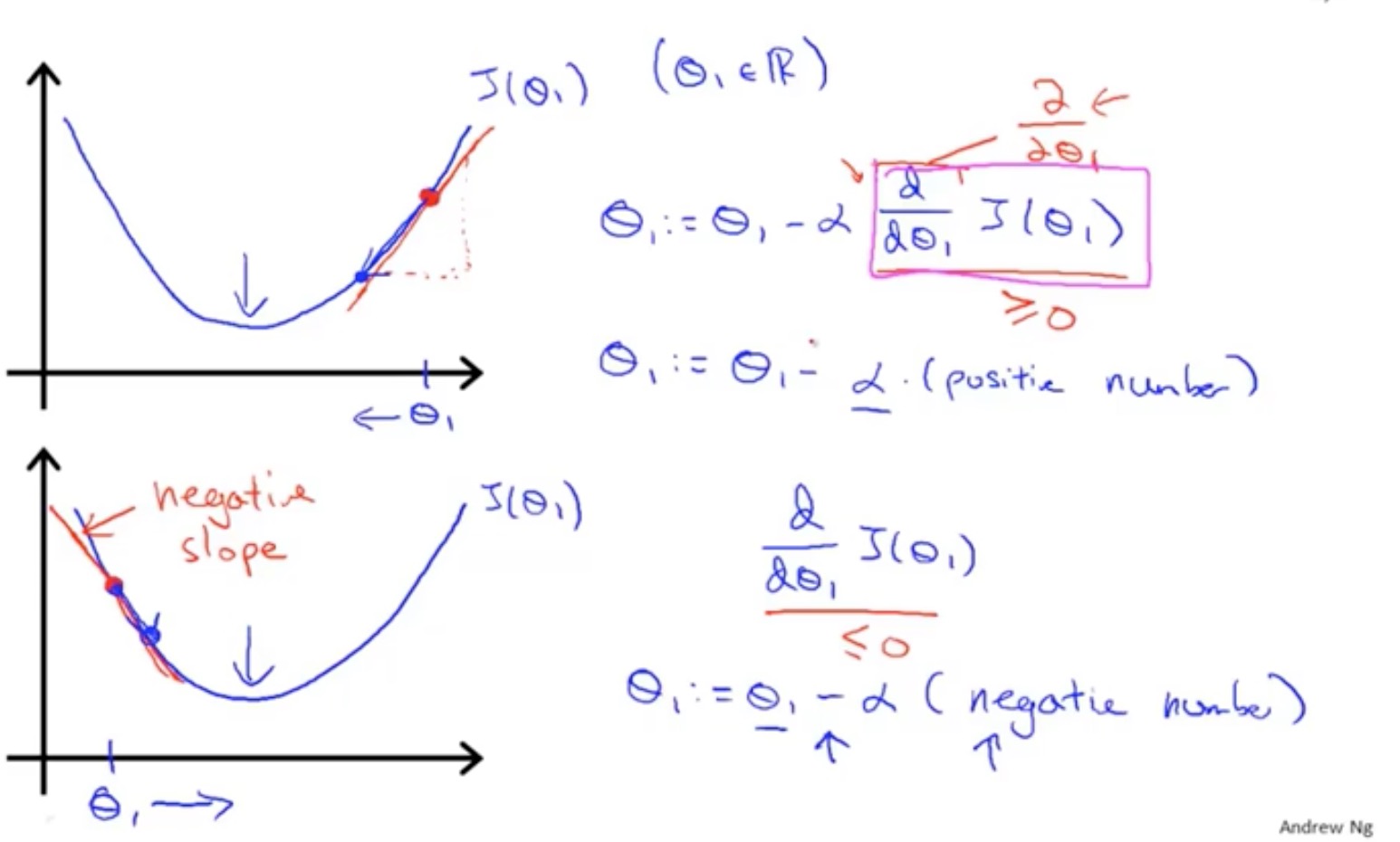
学习率大小的影响
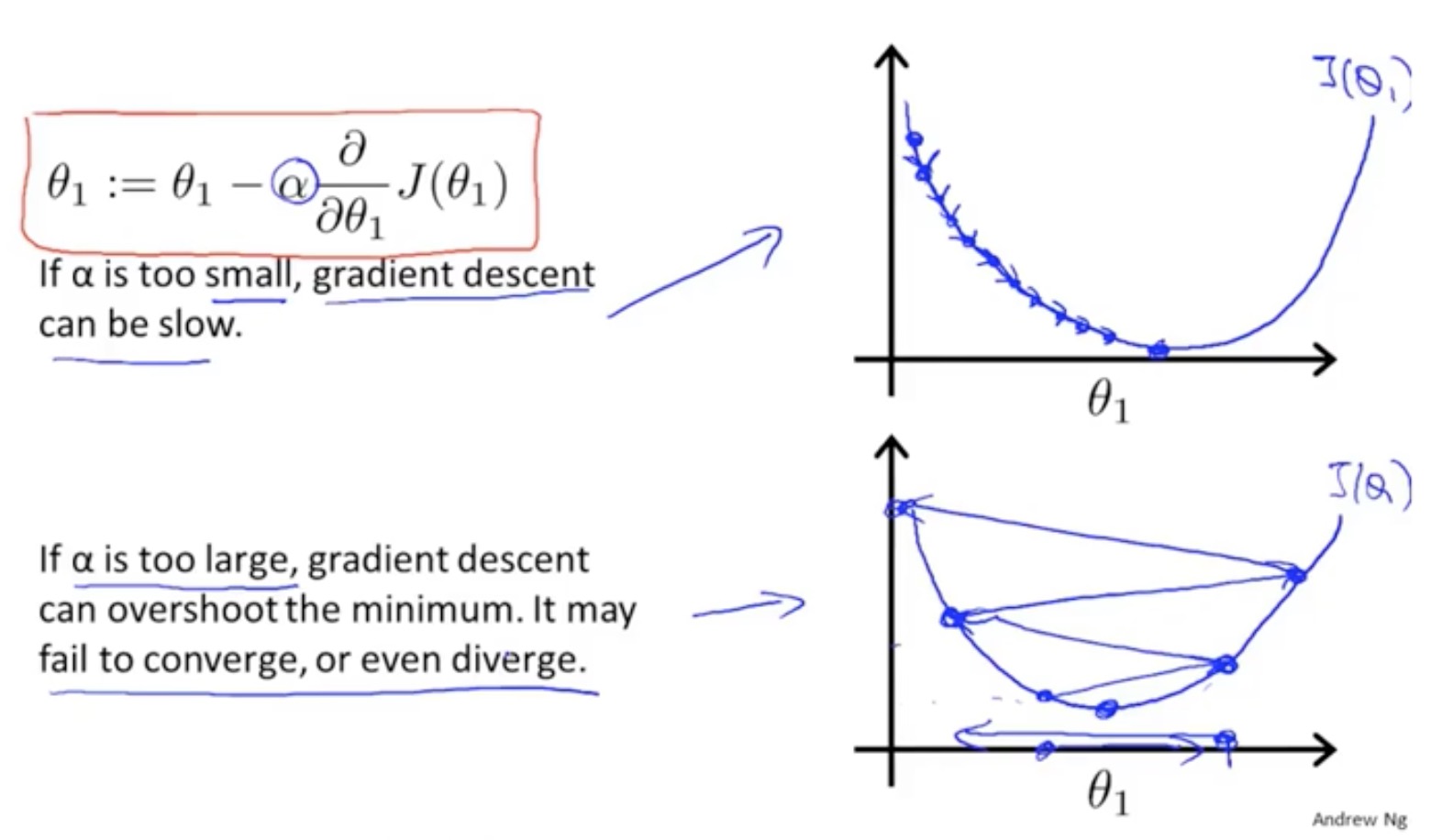
保持在了局部最优解
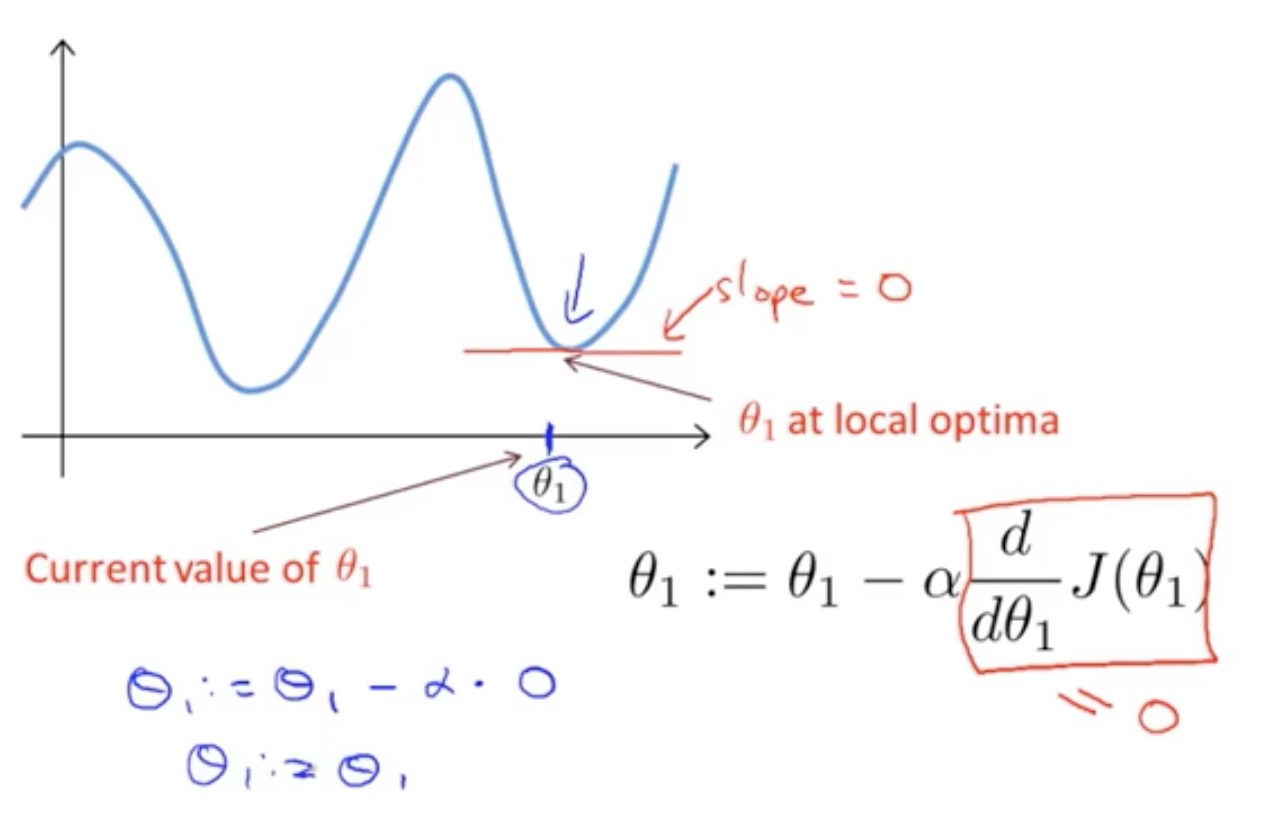
梯度下降与代价(损失)函数结合

判断j=0和j=1不同的情景
微积分的推导


多特征线性回归
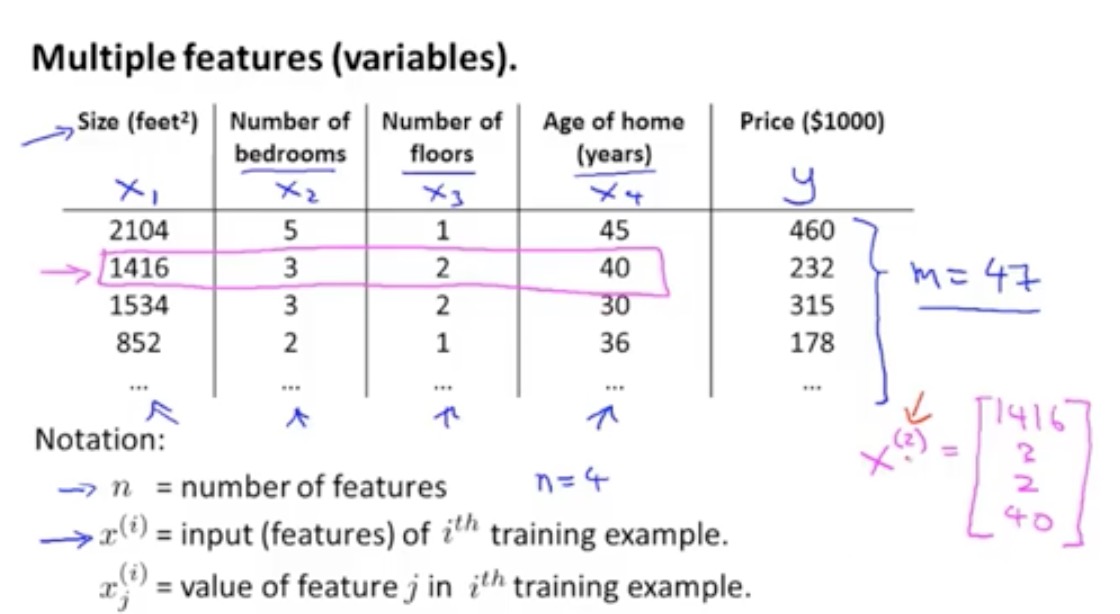
多特征假设函数
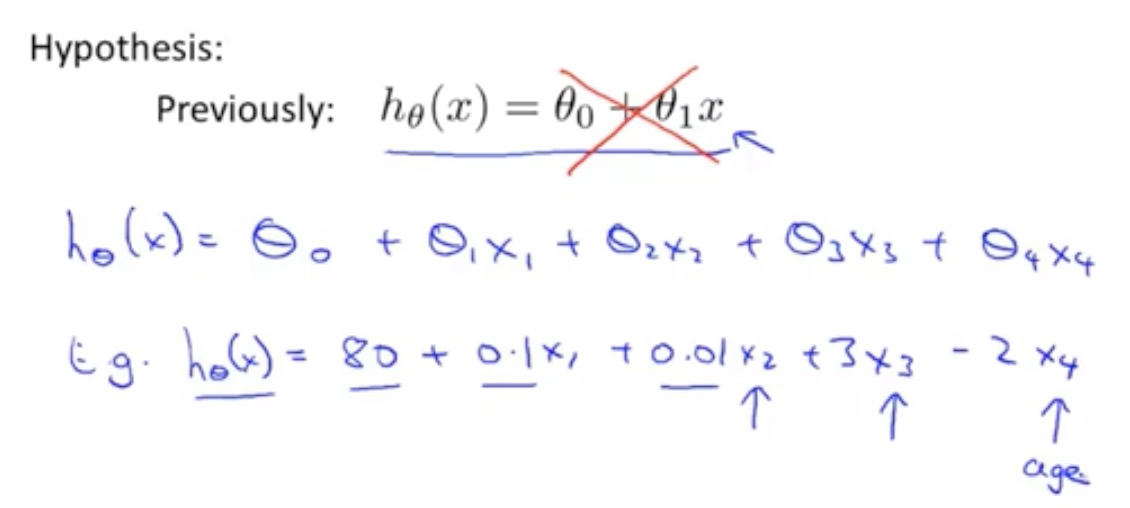

多元梯度下降法


选择合适的学习率和均值归一化特征向量

正规方程法

正则方程法的推导过程
https://blog.csdn.net/zoe9698/article/details/82419330
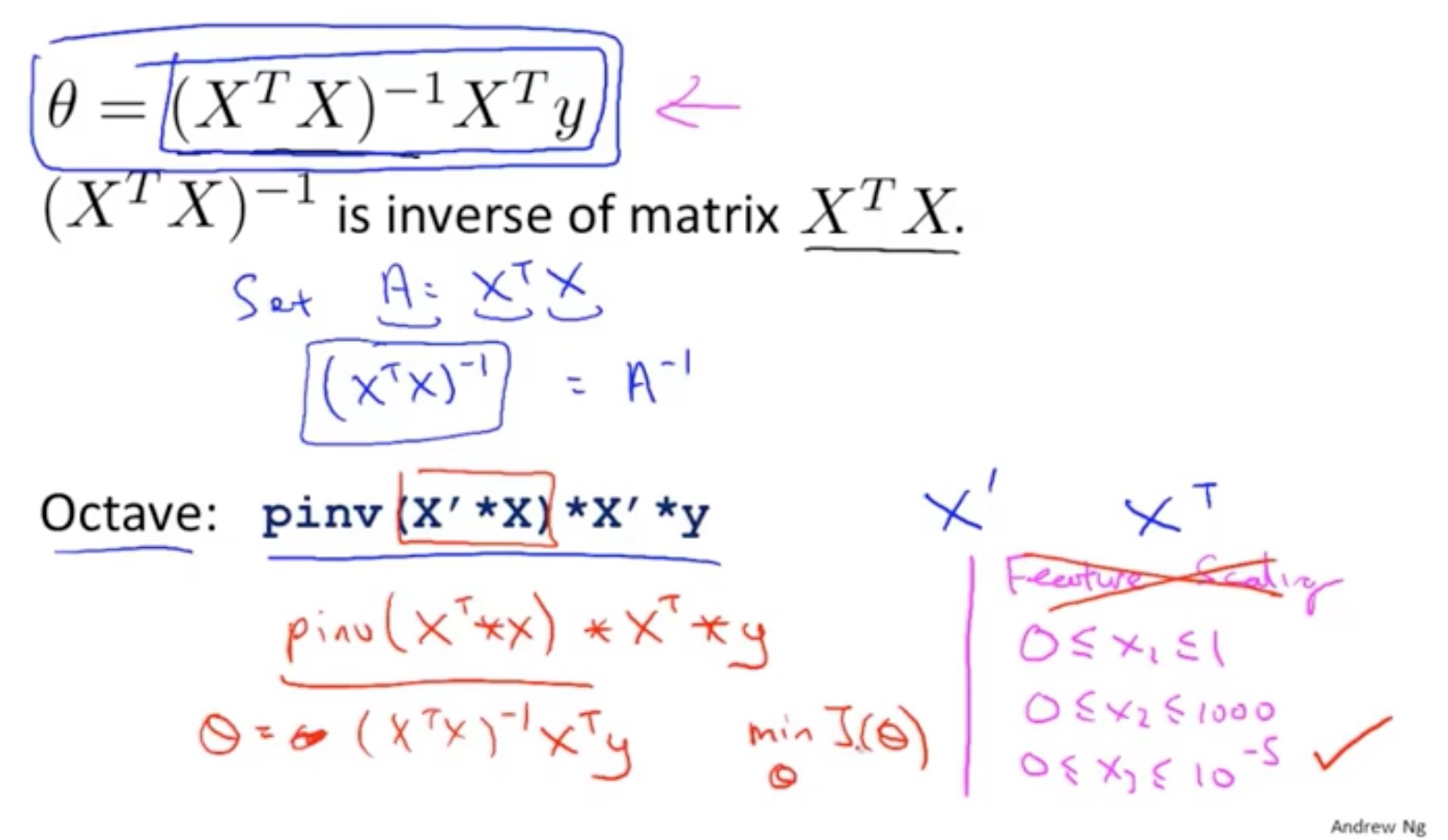
正则方程法在1w特征向量不实用性

正则方程法在不可逆矩阵的处理,删除多余特征向量

Logistic 回归
Logistic 与线性回归在分类问题上的局限性
监督学习,解决二分类问题。
分类的本质:在空间中找到一个决策边界来完成分类的决策
逻辑回归:线性回归可以预测连续值,但是不能解决分类问题,我们需要根据预测的结果判定其属于正类还是负类。所以逻辑回归就是将线性回归的(−∞,+∞) 结果,通过sigmoid函数映射到(0,1)之间。
线性回归回因特殊样本造成伪预测


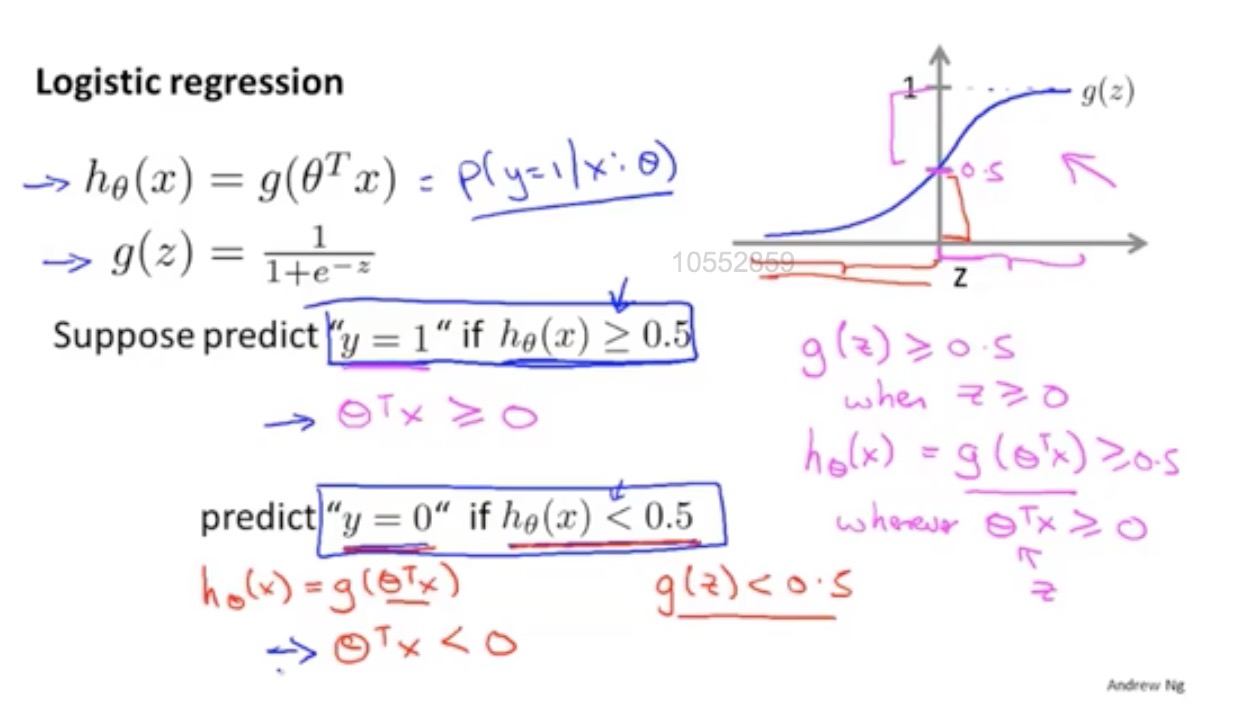
Logistic回归模型
g函数可为sigmod(logistic函数术语相同)

决策边界
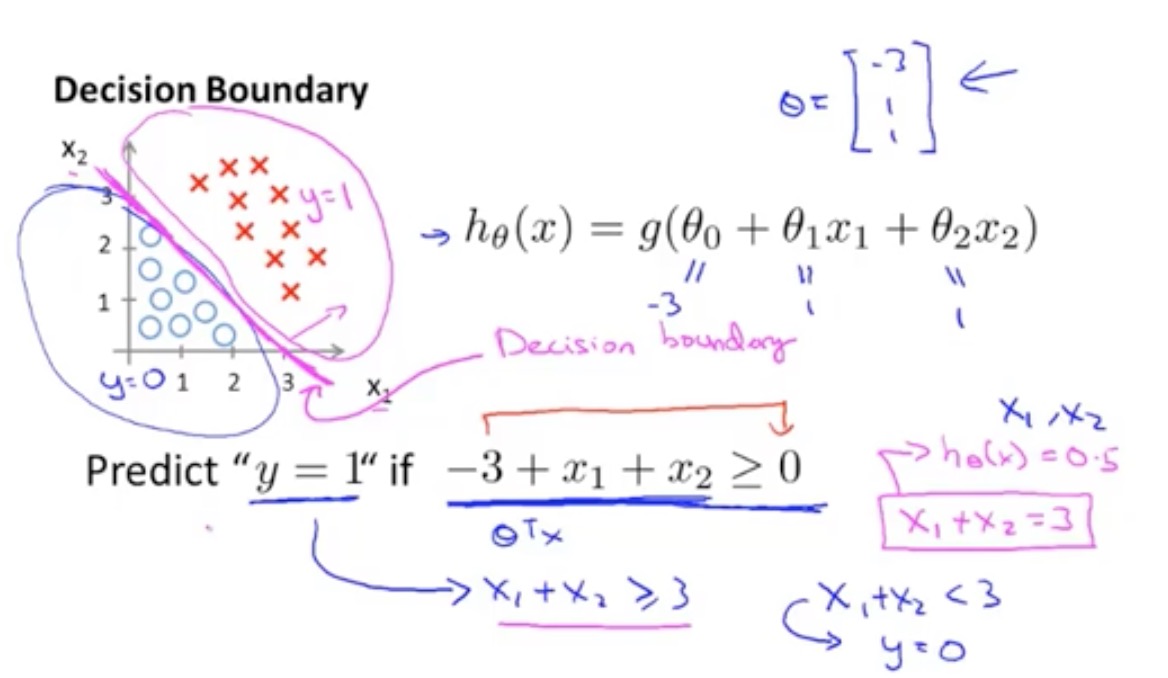

代价(损失)函数
线性回归的损失函数为平方损失函数,如果将其用于逻辑回归的损失函数
则其数学特性不好,有很多局部极小值,难以用梯度下降法求最优。
选用全局最优解
逻辑回归损失函数:对数损失函数
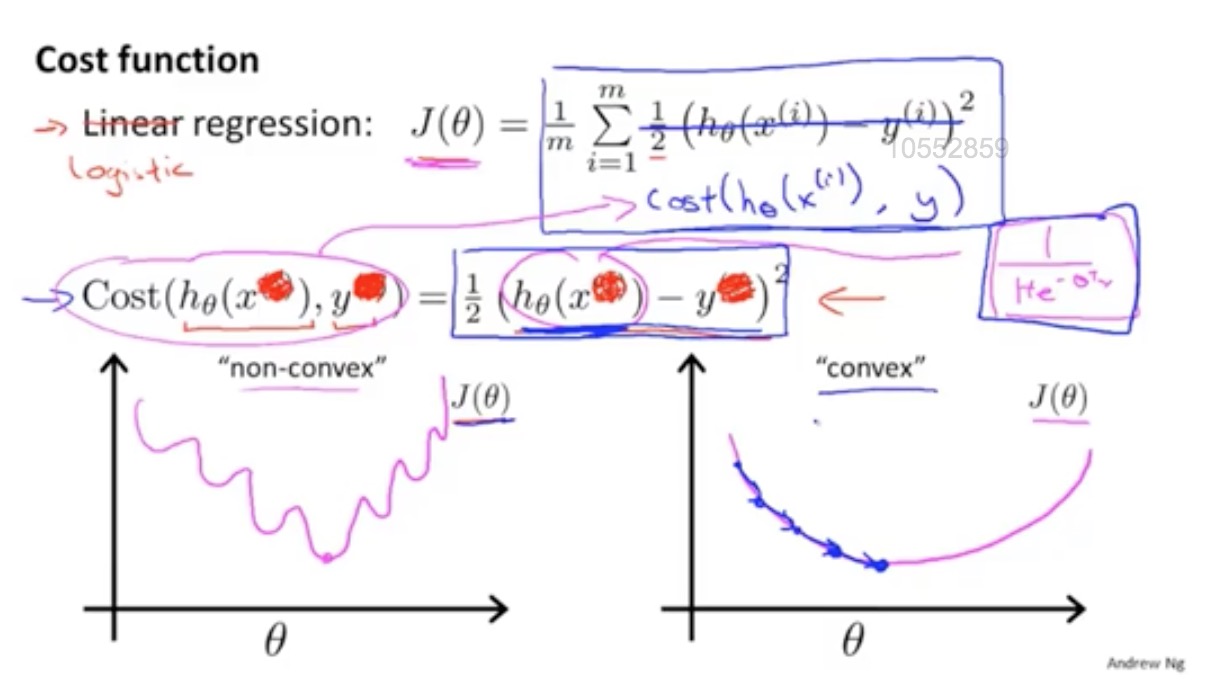
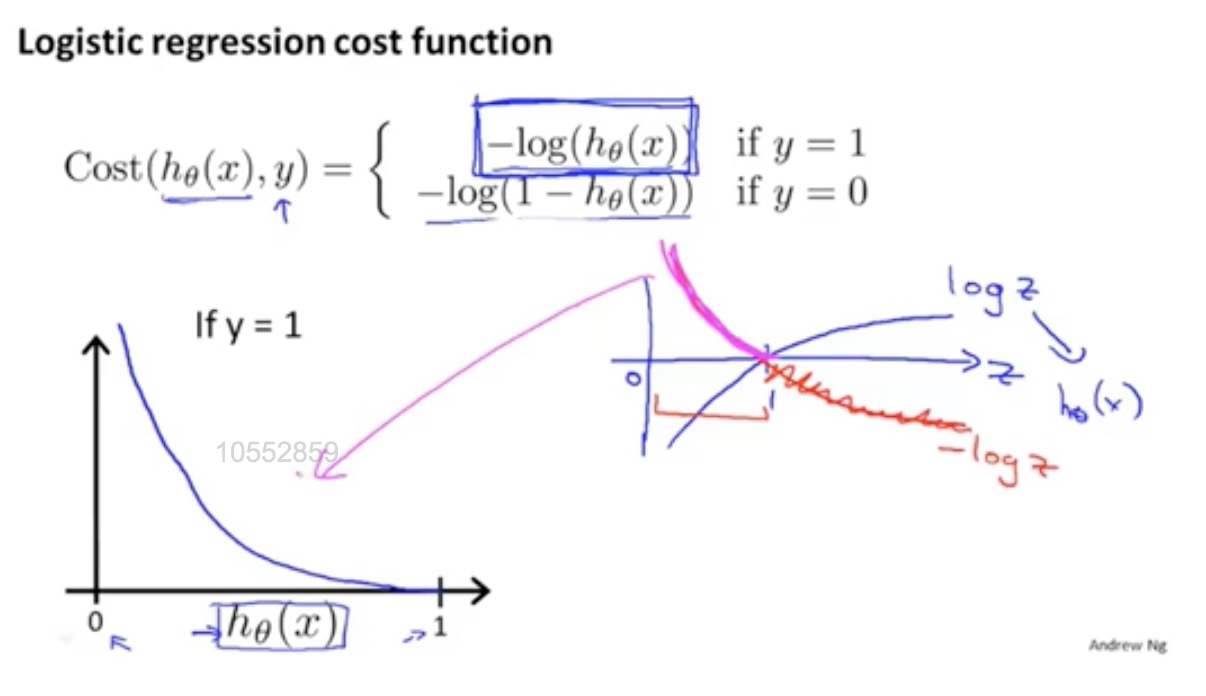
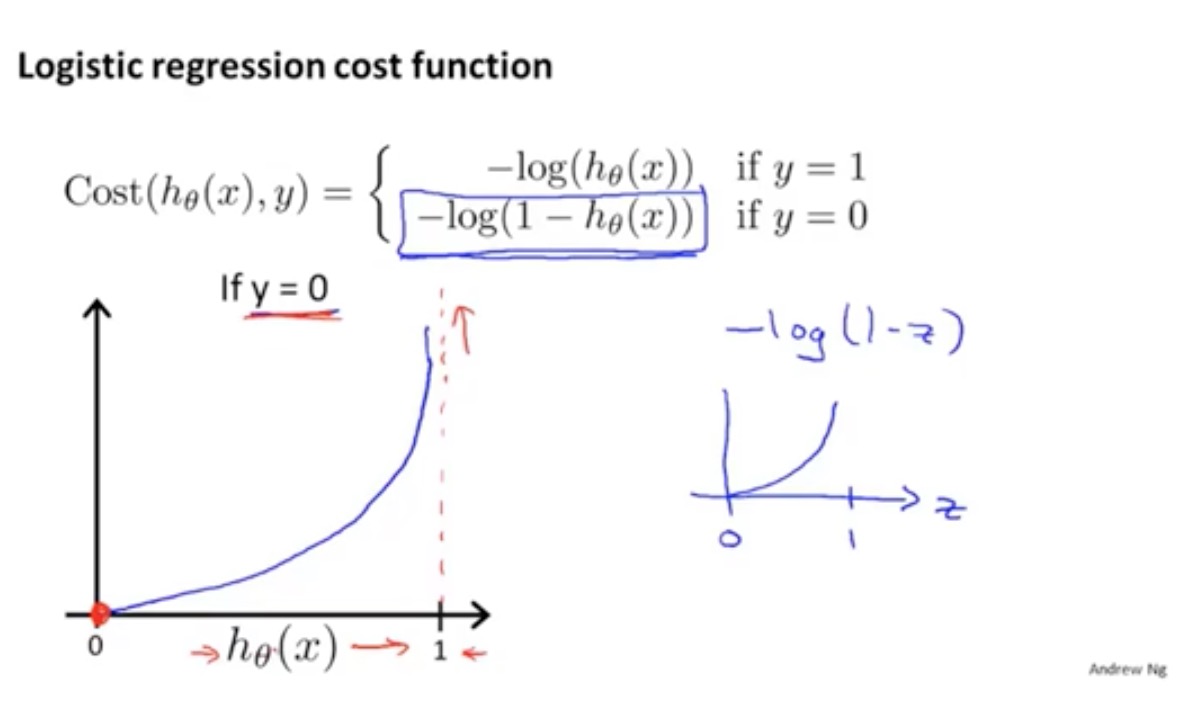
logistics代价函数推导

梯度下降


正则化
减少过度拟合问题
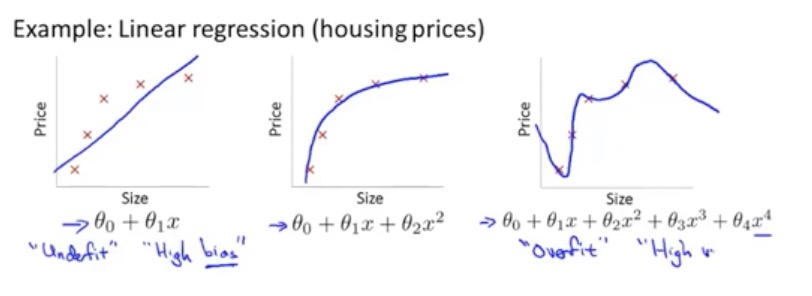
图一:欠拟合、导致拟合效果差
图二:二阶项, 拟合效果稍好
图三:四阶项,很好的拟合了数据集(过度拟合、高方差)
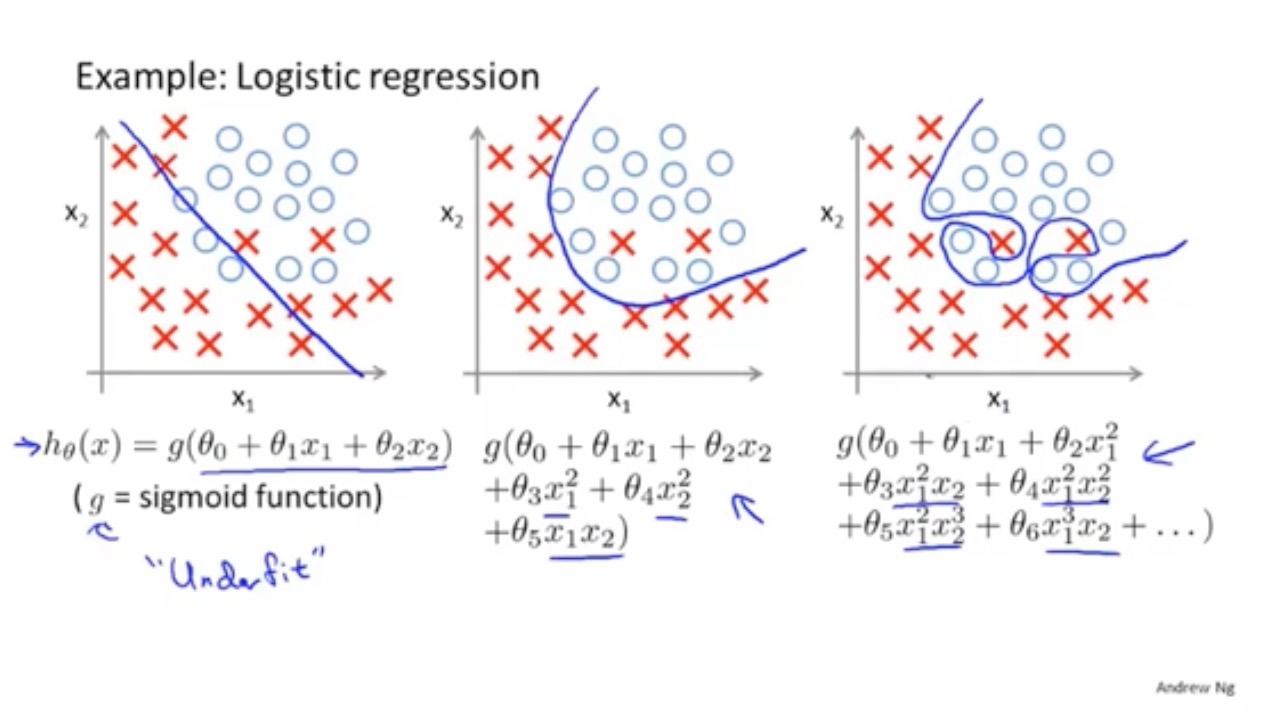
过拟合问题
特征数据少,样本数据过多,就会出现过拟合现象,泛化的不好

解决过拟合方案
模型选择算法, 哪些特征保留,哪些特征舍弃
正则化, 不希望舍弃掉,保留所有特征向量,但减少量级
正则化的运行
正则化增加新的一项,作用缩小每个参数

正则化参数选择很重要,如果过大,则只趋于一条直线

线性回归-正则化
代价(损失)函数

梯度下降
正则化推导

正规方程法


Logistic回归-正则化
logistics回归用正则避免过拟合现象
代价(损失)函数
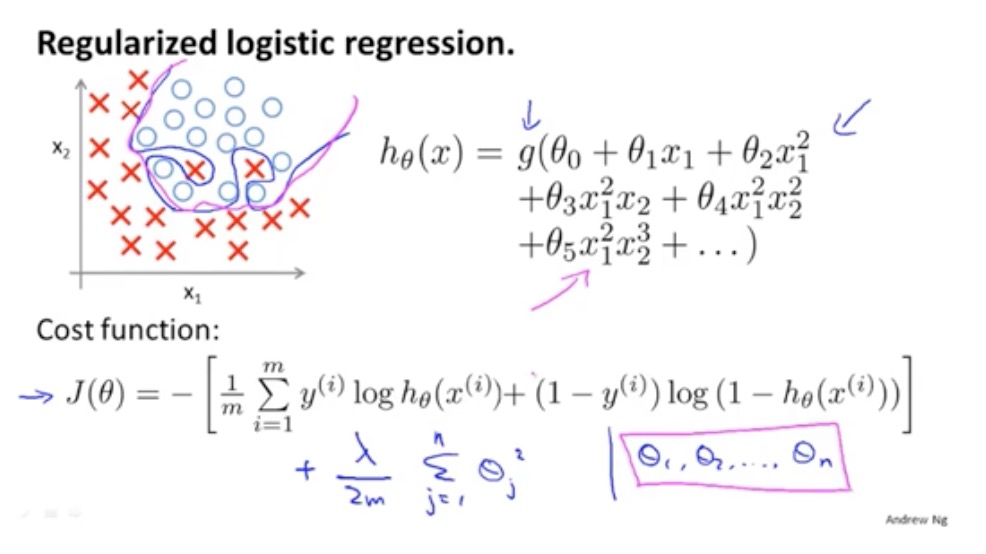
梯度下降

深度学习
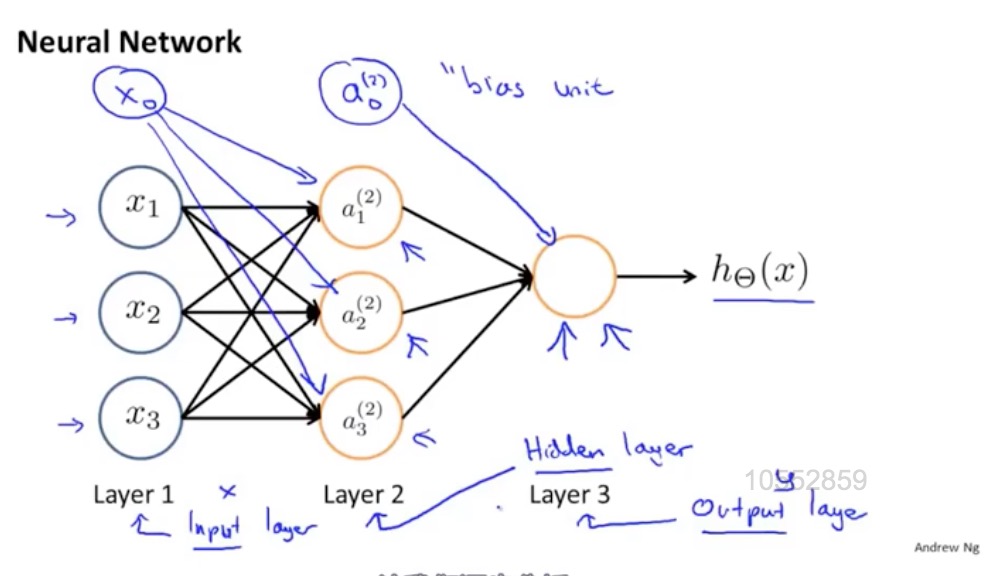
神经网络
因特征过多,logistics回归并不是一个好方法, 神经网络反而是一种非线性假设好的算法
神经网络最初发明制造能模拟大脑的机器,能解决机器学习不能解决的问题
神经元细胞结构

计算机模拟的神经元结构

神经网络模拟
权重也是函数的参数
1:正规方程式的推导?不可逆的矩阵如何处理?矩阵在什么情况下不可逆?
2:解释一下梯度下降法?
国内查看评论需要代理~