部分数据结构与算法分析
排序
插入排序 直接插入排序 直接插入排序基本思想是每一步将一个待排序的记录,插入到前面已经排好序的有序序列中去,直到插完所有元素为止。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 public static void insertionSort (int [] arr) for (int i = 1 ; i < arr.length; i++) { int j = i; while (j > 0 && arr[j] < arr[j - 1 ]) { swap(arr,j,j-1 ); j--; } } }
简单插入排序在最好情况下,需要比较n-1次,无需交换元素,时间复杂度为O(n);在最坏情况下,时间复杂度依然为O(n2)。
折半插入排序 折半插入排序是对直接插入排序的简单改进,对于直接插入排序而言,当第i-1趟需要将第i个元素插入前面的0~i-1个元素序列中时,总是需要从i-1个元素开始,逐个比较每个元素,直到找到它的位置。这显然没有利用前面0~i-1个元素已经有序这个特点,而折半插入排序则改进了这一点。
对于折半插入排序而言,当需要插入第i个元素时,它不会逐个进行比较每个元素,而是:
(1)计算0~i-1索引的中间点,也就是用i索引处的元素和(0+i-1)/2索引处的元素进行比较,如果i索引处的元素值大,就直接在(0+i-1)/2~i-1半个范围内进行搜索;反之在0~(0+i-1)/2半个范围内搜索,这就是所谓的折半;
(2)在半个范围内搜索时,按照(1)的方法不断地进行折半搜索,这样就可以将搜索范围缩小到1/2、1/4、1/8…,从而快速的确定插入位置;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 package com.liuhao.sort; import java.util.Arrays; public class BinaryInsertSort public static void binaryInsertSort (DataWrap[] data) int arrayLength = data.length; for (int i=1 ; i<arrayLength; i++){ DataWrap tmp = data[i]; int low = 0 ; int high = i-1 ; while (low <= high){ int mid = (low + high) / 2 ; if (tmp.compareTo(data[mid]) > 0 ){ low = mid + 1 ; } else { high = mid - 1 ; } } for (int j=i; j>low ; j--){ data[j] = data[j-1 ]; } data[low] = tmp; System.out.println(Arrays.toString(data)); } } public static void main (String[] args) DataWrap[] data = { new DataWrap(21 , "" ) ,new DataWrap(30 , "" ) ,new DataWrap(49 , "" ) ,new DataWrap(30 , "*" ) ,new DataWrap(16 , "" ) ,new DataWrap(9 , "" ) }; System.out.println("排序之前:" + Arrays.toString(data)); binaryInsertSort(data); System.out.println("排序之后:" + Arrays.toString(data)); } }
折半插入排序减少了关键字的比较次数,但是记录的移动次数不变,其时间复杂度与直接插入排序相同。
希尔排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 package sortdemo;import java.util.Arrays;public class ShellSort public static void main (String []args) int []arr ={1 ,4 ,2 ,7 ,9 ,8 ,3 ,6 }; sort(arr); System.out.println(Arrays.toString(arr)); int []arr1 ={1 ,4 ,2 ,7 ,9 ,8 ,3 ,6 }; sort1(arr1); System.out.println(Arrays.toString(arr1)); } public static void sort (int []arr) for (int gap=arr.length/2 ;gap>0 ;gap/=2 ){ for (int i=gap;i<arr.length;i++){ int j = i; while (j-gap>=0 && arr[j]<arr[j-gap]){ swap(arr,j,j-gap); j-=gap; } } } } public static void sort1 (int []arr) for (int gap=arr.length/2 ;gap>0 ;gap/=2 ){ for (int i=gap;i<arr.length;i++){ int j = i; int temp = arr[j]; if (arr[j]<arr[j-gap]){ while (j-gap>=0 && temp<arr[j-gap]){ arr[j] = arr[j-gap]; j-=gap; } arr[j] = temp; } } } } public static void swap (int []arr,int a,int b) arr[a] = arr[a]+arr[b]; arr[b] = arr[a]-arr[b]; arr[a] = arr[a]-arr[b]; } }
交换排序 冒泡排序 冒泡排序的基本思想是,对相邻的元素进行两两比较,顺序相反则进行交换,这样,每一趟会将最小或最大的元素“浮”到顶端,最终达到完全有序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public static void bubbleSort (int [] arr) for (int i = 0 ; i < arr.length - 1 ; i++) { boolean flag = true ; for (int j = 0 ; j < arr.length - 1 - i; j++) { if (arr[j] > arr[j + 1 ]) { swap(arr,j,j+1 ); flag = false ; } } if (flag) { break ; } } }
根据上面这种冒泡实现,若原数组本身就是有序的(这是最好情况),仅需n-1次比较就可完成;若是倒序,比较次数为 n-1+n-2+…+1=n(n-1)/2,交换次数和比较次数等值。
综合来看冒泡排序性能还还是稍差于上面那种选择排序的。
快速排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 void quick_sort (int a[], int l, int r) if (l < r) { int i,j,x; i = l; j = r; x = a[i]; while (i < j) { while (i < j && a[j] > x) j--; if (i < j) a[i++] = a[j]; while (i < j && a[i] < x) i++; if (i < j) a[j--] = a[i]; } a[i] = x; quick_sort(a, l, i-1 ); quick_sort(a, i+1 , r); } }
快速排序稳定性
快速排序是不稳定的算法,它不满足稳定算法的定义。
快速排序时间复杂度
快速排序的时间复杂度在最坏情况下是O(N2),平均的时间复杂度是O(N*lgN)。
(01) 为什么最少是lg(N+1)次?快速排序是采用的分治法进行遍历的,我们将它看作一棵二叉树,它需要遍历的次数就是二叉树的深度,而根据完全二叉树的定义,它的深度至少是lg(N+1)。因此,快速排序的遍历次数最少是lg(N+1)次。
(02) 为什么最多是N次?这个应该非常简单,还是将快速排序看作一棵二叉树,它的深度最大是N。因此,快读排序的遍历次数最多是N次。
选择排序 简单选择排序
简单选择排序是最简单直观的一种算法,基本思想为每一趟从待排序的数据元素中选择最小(或最大)的一个元素作为首元素,直到所有元素排完为止,简单选择排序是不稳定排序。
在算法实现时,每一趟确定最小元素的时候会通过不断地比较交换来使得首位置为当前最小,交换是个比较耗时的操作。其实我们很容易发现,在还未完全确定当前最小元素之前,这些交换都是无意义的。我们可以通过设置一个变量min,每一次比较仅存储较小元素的数组下标,当轮循环结束之后,那这个变量存储的就是当前最小元素的下标,此时再执行交换操作即可。代码实现很简单,一起来看下。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public static void selectSort (int [] arr) for (int i = 0 ; i < arr.length - 1 ; i++) { int min = i; for (int j = i + 1 ; j < arr.length; j++) { if (arr[j] < arr[min]) { min = j; } } if (min != i) { swap(arr,min,i); } } }
堆排序 堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆
堆排序的基本思想是:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 package sortdemo;import java.util.Arrays;public class HeapSort public static void main (String []args) int []arr = {9 ,8 ,7 ,6 ,5 ,4 ,3 ,2 ,1 }; sort(arr); System.out.println(Arrays.toString(arr)); } public static void sort (int []arr) for (int i=arr.length/2 -1 ;i>=0 ;i--){ adjustHeap(arr,i,arr.length); } for (int j=arr.length-1 ;j>0 ;j--){ swap(arr,0 ,j); adjustHeap(arr,0 ,j); } } public static void adjustHeap (int []arr,int i,int length) int temp = arr[i]; for (int k=i*2 +1 ;k<length;k=k*2 +1 ){ if (k+1 <length && arr[k]<arr[k+1 ]){ k++; } if (arr[k] >temp){ arr[i] = arr[k]; i = k; }else { break ; } } arr[i] = temp; } public static void swap (int []arr,int a ,int b) int temp=arr[a]; arr[a] = arr[b]; arr[b] = temp; } }
计数排序 计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
算法的步骤如下
(1)找出待排序的数组中最大和最小的元素
(2)统计数组中每个值为i的元素出现的次数,存入数组C的第i项
(3)对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
(4)反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 public class CountingSort implements IArraySort @Override public int [] sort(int [] sourceArray) throws Exception { int [] arr = Arrays.copyOf(sourceArray, sourceArray.length); int maxValue = getMaxValue(arr); return countingSort(arr, maxValue); } private int [] countingSort(int [] arr, int maxValue) { int bucketLen = maxValue + 1 ; int [] bucket = new int [bucketLen]; for (int value : arr) { bucket[value]++; } int sortedIndex = 0 ; for (int j = 0 ; j < bucketLen; j++) { while (bucket[j] > 0 ) { arr[sortedIndex++] = j; bucket[j]--; } } return arr; } private int getMaxValue (int [] arr) int maxValue = arr[0 ]; for (int value : arr) { if (maxValue < value) { maxValue = value; } } return maxValue; } }
桶排序 桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效,我们需要做到这两点:
在额外空间充足的情况下,尽量增大桶的数量
什么时候最快
当输入的数据可以均匀的分配到每一个桶中。
什么时候最慢
当输入的数据被分配到了同一个桶中。
元素分布在桶中
元素在每个桶中排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 public class BucketSort implements IArraySort private static final InsertSort insertSort = new InsertSort(); @Override public int [] sort(int [] sourceArray) throws Exception { int [] arr = Arrays.copyOf(sourceArray, sourceArray.length); return bucketSort(arr, 5 ); } private int [] bucketSort(int [] arr, int bucketSize) throws Exception { if (arr.length == 0 ) { return arr; } int minValue = arr[0 ]; int maxValue = arr[0 ]; for (int value : arr) { if (value < minValue) { minValue = value; } else if (value > maxValue) { maxValue = value; } } int bucketCount = (int ) Math.floor((maxValue - minValue) / bucketSize) + 1 ; int [][] buckets = new int [bucketCount][0 ]; for (int i = 0 ; i < arr.length; i++) { int index = (int ) Math.floor((arr[i] - minValue) / bucketSize); buckets[index] = arrAppend(buckets[index], arr[i]); } int arrIndex = 0 ; for (int [] bucket : buckets) { if (bucket.length <= 0 ) { continue ; } bucket = insertSort.sort(bucket); for (int value : bucket) { arr[arrIndex++] = value; } } return arr; } private int [] arrAppend(int [] arr, int value) { arr = Arrays.copyOf(arr, arr.length + 1 ); arr[arr.length - 1 ] = value; return arr; } }
归并排序 归并排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 package sortdemo;import java.util.Arrays;public class MergeSort public static void main (String []args) int []arr = {9 ,8 ,7 ,6 ,5 ,4 ,3 ,2 ,1 }; sort(arr); System.out.println(Arrays.toString(arr)); } public static void sort (int []arr) int []temp = new int [arr.length]; sort(arr,0 ,arr.length-1 ,temp); } private static void sort (int [] arr,int left,int right,int []temp) if (left<right){ int mid = (left+right)/2 ; sort(arr,left,mid,temp); sort(arr,mid+1 ,right,temp); merge(arr,left,mid,right,temp); } } private static void merge (int [] arr,int left,int mid,int right,int [] temp) int i = left; int j = mid+1 ; int t = 0 ; while (i<=mid && j<=right){ if (arr[i]<=arr[j]){ temp[t++] = arr[i++]; }else { temp[t++] = arr[j++]; } } while (i<=mid){ temp[t++] = arr[i++]; } while (j<=right){ temp[t++] = arr[j++]; } t = 0 ; while (left <= right){ arr[left++] = temp[t++]; } } }
基数排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 public class RadixSort implements IArraySort @Override public int [] sort(int [] sourceArray) throws Exception { int [] arr = Arrays.copyOf(sourceArray, sourceArray.length); int maxDigit = getMaxDigit(arr); return radixSort(arr, maxDigit); } private int getMaxDigit (int [] arr) int maxValue = getMaxValue(arr); return getNumLenght(maxValue); } private int getMaxValue (int [] arr) int maxValue = arr[0 ]; for (int value : arr) { if (maxValue < value) { maxValue = value; } } return maxValue; } protected int getNumLenght (long num) if (num == 0 ) { return 1 ; } int lenght = 0 ; for (long temp = num; temp != 0 ; temp /= 10 ) { lenght++; } return lenght; } private int [] radixSort(int [] arr, int maxDigit) { int mod = 10 ; int dev = 1 ; for (int i = 0 ; i < maxDigit; i++, dev *= 10 , mod *= 10 ) { int [][] counter = new int [mod * 2 ][0 ]; for (int j = 0 ; j < arr.length; j++) { int bucket = ((arr[j] % mod) / dev) + mod; counter[bucket] = arrayAppend(counter[bucket], arr[j]); } int pos = 0 ; for (int [] bucket : counter) { for (int value : bucket) { arr[pos++] = value; } } } return arr; } private int [] arrayAppend(int [] arr, int value) { arr = Arrays.copyOf(arr, arr.length + 1 ); arr[arr.length - 1 ] = value; return arr; } }
数组 二分法 总结 链表 链表相加 21. 合并两个有序链表 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
1 2 输入:l1 = [1,2,4], l2 = [1,3,4] 输出:[1,1,2,3,4,4]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution public ListNode mergeTwoLists (ListNode l1, ListNode l2) ListNode dummyHead = new ListNode(0 ); ListNode cur = dummyHead; while (l1 != null && l2 != null ) { if (l1.val < l2.val) { cur.next = l1; cur = cur.next; l1 = l1.next; } else { cur.next = l2; cur = cur.next; l2 = l2.next; } } if (l1 == null ) { cur.next = l2; } else { cur.next = l1; } return dummyHead.next; } }
23. 合并K个升序链表 给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
1 2 3 4 5 6 7 8 9 10 输入:lists = [[1,4,5],[1,3,4],[2,6]] 输出:[1,1,2,3,4,4,5,6] 解释:链表数组如下: [ 1->4->5, 1->3->4, 2->6 ] 将它们合并到一个有序链表中得到。 1->1->2->3->4->4->5->6
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class Solution public ListNode mergeKLists (ListNode[] lists) if (lists.length == 0 ) { return null ; } ListNode dummyHead = new ListNode(0 ); ListNode curr = dummyHead; PriorityQueue<ListNode> pq = new PriorityQueue<>(new Comparator<ListNode>() { @Override public int compare (ListNode o1, ListNode o2) return o1.val - o2.val; } }); for (ListNode list : lists) { if (list == null ) { continue ; } pq.add(list); } while (!pq.isEmpty()) { ListNode nextNode = pq.poll(); curr.next = nextNode; curr = curr.next; if (nextNode.next != null ) { pq.add(nextNode.next); } } return dummyHead.next; } }
两数相加 2.两数相加 给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
1 2 3 4 5 6 7 8 9 输入:l1 = [2,4,3], l2 = [5,6,4] 输出:[7,0,8] 解释:342 + 465 = 807 输入:l1 = [0], l2 = [0] 输出:[0] 输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9] 输出:[8,9,9,9,0,0,0,1]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution public ListNode addTwoNumbers (ListNode l1, ListNode l2) ListNode root = new ListNode(0 ); ListNode cursor = root; int carry = 0 ; while (l1 != null || l2 != null || carry != 0 ) { int l1Val = l1 != null ? l1.val : 0 ; int l2Val = l2 != null ? l2.val : 0 ; int sumVal = l1Val + l2Val + carry; carry = sumVal / 10 ; ListNode sumNode = new ListNode(sumVal % 10 ); cursor.next = sumNode; cursor = sumNode; if (l1 != null ) l1 = l1.next; if (l2 != null ) l2 = l2.next; } return root.next; } }
445. 两数相加 II 给你两个 非空 链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。
1 2 3 4 5 6 7 8 输入:l1 = [7,2,4,3], l2 = [5,6,4] 输出:[7,8,0,7] 输入:l1 = [2,4,3], l2 = [5,6,4] 输出:[8,0,7] 输入:l1 = [0], l2 = [0] 输出:[0]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution public ListNode addTwoNumbers (ListNode l1, ListNode l2) Stack<Integer> stack1 = new Stack<>(); Stack<Integer> stack2 = new Stack<>(); while (l1 != null ) { stack1.push(l1.val); l1 = l1.next; } while (l2 != null ) { stack2.push(l2.val); l2 = l2.next; } int carry = 0 ; ListNode head = null ; while (!stack1.isEmpty() || !stack2.isEmpty() || carry > 0 ) { int sum = carry; sum += stack1.isEmpty()? 0 : stack1.pop(); sum += stack2.isEmpty()? 0 : stack2.pop(); ListNode node = new ListNode(sum % 10 ); node.next = head; head = node; carry = sum / 10 ; } return head; } }
链表反转 206. 反转链表 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
1 2 输入:head = [1,2,3,4,5] 输出:[5,4,3,2,1]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution public ListNode reverseList (ListNode head) ListNode prev = null ; ListNode curr = head; while (curr != null ) { ListNode nextTemp = curr.next; curr.next = prev; prev = curr; curr = nextTemp; } return prev; } }
92. 反转链表 II 给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution {public : ListNode * successor = nullptr ; ListNode* reverseN (ListNode* head, int end) { if (head->next == NULL || end == 1 ) { successor = head->next; return head; }; ListNode* last = reverseN(head->next, end - 1 ); head->next->next = head; head->next = successor; return last; } ListNode* reverseBetween (ListNode* head, int start, int end) { if (start == 1 ){ return reverseN(head, end); } head->next = reverseBetween(head->next, start-1 , end-1 ); return head; } };
总结 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 ListNode* reverse (ListNode* head) { if (head->next == NULL ) return head; ListNode* last = reverse(head->next); head->next->next = head; head->next= nullptr ; return last; } ListNode * successor = nullptr ; ListNode* reverseN (ListNode* head, int end) { if (head->next == NULL || end == 1 ) { successor = head->next; return head; }; ListNode* last = reverseN(head->next, end - 1 ); head->next->next = head; head->next = successor; return last; } ListNode* reverseAll (ListNode* head) { if (head->next == nullptr ){ return head; } ListNode* last = reverseAll(head->next); head->next->next = head; head->next = nullptr ; return last; } ListNode* reverseNEnd (ListNode* head, int n) { if (n == 1 ){ return reverseAll(head); } head->next = reverseNEnd(head->next, n-1 ); return head; } ListNode* reverseBetween (ListNode* head, int start, int end) { if (start == 1 ){ return reverseN(head, end); } head->next = reverseBetween(head->next, start-1 , end-1 ); return head; } ListNode* reverseNGroup (ListNode* head, int end) { if (head->next == NULL || end == 1 ) { successor = head->next; return head; }; ListNode* last = reverseN(head->next, end - 1 ); head->next->next = head; head->next = successor; return last; }
链表旋转 61. 旋转链表 给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。
1 2 输入:head = [1,2,3,4,5], k = 2 输出:[4,5,1,2,3]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution public ListNode rotateRight (ListNode head, int k) if (head == null || head.next == null || k == 0 ) return head; int count = 1 ; ListNode tmp = head; while (tmp.next != null ) { count++; tmp = tmp.next; } k %= count; if (k == 0 ) return head; tmp.next = head; for (int i = 0 ; i < count - k; i++) { tmp = tmp.next; } ListNode newHead = tmp.next; tmp.next = null ; return newHead; } }
判断环形 141. 环形链表 给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
如果链表中存在环,则返回 true 。 否则,返回 false 。
1 2 3 输入:head = [3,2,0,-4], pos = 1 输出:true 解释:链表中有一个环,其尾部连接到第二个节点。
快慢指针
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution {public : bool hasCycle (ListNode* head) ListNode* fast = head, * slow = head; while (fast && fast->next) { fast = fast->next->next; slow = slow->next; if (slow == fast) return true ; } return false ; } };
142. 环形链表 II 给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
1 2 3 输入:head = [3,2,0,-4], pos = 1 输出:返回索引为 1 的链表节点 解释:链表中有一个环,其尾部连接到第二个节点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public class Solution public ListNode detectCycle (ListNode head) ListNode slow = head; ListNode fast = head; while (fast != null && fast.next != null ) { slow = slow.next; fast = fast.next.next; if (slow == fast) { ListNode index1 = fast; ListNode index2 = head; while (index1 != index2) { index1 = index1.next; index2 = index2.next; } return index1; } } return null ; } }
链表划分 725. 分隔链表 给你一个头结点为 head 的单链表和一个整数 k ,请你设计一个算法将链表分隔为 k 个连续的部分。
这 k 个部分应该按照在链表中出现的顺序排列,并且排在前面的部分的长度应该大于或等于排在后面的长度。
1 2 3 4 输入:head = [1,2,3,4,5,6,7,8,9,10], k = 3 输出:[[1,2,3,4],[5,6,7],[8,9,10]] 解释: 输入被分成了几个连续的部分,并且每部分的长度相差不超过 1 。前面部分的长度大于等于后面部分的长度。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution public ListNode[] splitListToParts(ListNode head, int k) { int len = 0 ; ListNode p = head; while (p != null ) { len++; p = p.next; } int a = len / k, b = len % k; p = head; ListNode[] ans = new ListNode[k]; for (int i = 0 ; i < k; ++i) { ans[i] = p; if (p == null ) continue ; ListNode temp = p; for (int j = 1 ; j < a + (b > 0 ? 1 : 0 ); ++j) { temp = temp.next; } p = temp.next; temp.next = null ; b--; } return ans; } }
链表判&去重 234. 回文链表 给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。
1 2 输入:head = [1,2,2,1] 输出:true
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution public boolean isPalindrome (ListNode head) if (head == null || head.next == null ) { return true ; } ListNode fast = head; ListNode slow = head; while (fast.next != null && fast.next.next != null ) { fast = fast.next.next; slow = slow.next; } slow = reverse(slow.next); while (slow != null ) { if (head.val != slow.val) { return false ; } head = head.next; slow = slow.next; } return true ; } private ListNode reverse (ListNode head) if (head.next == null ) { return head; } ListNode newHead = reverse(head.next); head.next.next = head; head.next = null ; return newHead; } }
字符串 字符串变换查找 滑动窗口 3.无重复字符的最长字串 给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
1 2 3 输入: s = "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
1 2 3 输入: s = "bbbbb" 输出: 1 解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
1 2 3 4 输入: s = "pwwkew" 输出: 3 解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。 请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution public int lengthOfLongestSubstring (String s) int [] last = new int [128 ]; for (int i = 0 ; i < 128 ; i++) { last[i] = -1 ; } int n = s.length(); int res = 0 ; int start = 0 ; for (int i = 0 ; i < n; i++) { int index = s.charAt(i); start = Math.max(start, last[index] + 1 ); res = Math.max(res, i - start + 1 ); last[index] = i; } return res; } }
76.最小覆盖子串 给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “” 。
注意
1 2 输入:s = "ADOBECODEBANC", t = "ABC" 输出:"BANC"
1 2 输入:s = "a", t = "a" 输出:"a"
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class Solution {public : string minWindow (string s, string t) unordered_map <char , int > h; for (const auto &c : t) h[c]++; int n = s.size(); int cnt = 0 ; int i = 0 , j = 0 ; int len = INT_MAX; int minst = 0 ; while (j < n) { char c = s[j]; if (h.count(c)) { h[c]--; if (h[c] == 0 ) cnt++; } while (cnt == h.size()) { int size = j - i + 1 ; if (size < len) { len = size; minst = i; } char b = s[i]; if (h.count(b)) { h[b]++; if (h[b] > 0 ) cnt--; } i++; } j++; } string res = len == INT_MAX ? "" : s.substr(minst, len); return res; } };
567.字符串的排列 给你两个字符串 s1 和 s2 ,写一个函数来判断 s2 是否包含 s1 的排列。如果是,返回 true;否则,返回 false 。
1 2 3 输入:s1 = "ab" s2 = "eidbaooo" 输出:true 解释:s2 包含 s1 的排列之一 ("ba").
1 2 输入:s1= "ab" s2 = "eidboaoo" 输出:false
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class Solution {public : bool checkInclusion (string s1, string s2) if (s1.size() > s2.size()) return false ; int windowSize = s1.size(); vector <int > hashmap1(26 , 0 ); vector <int > hashmap2(26 , 0 ); for (int i = 0 ; i < windowSize; i++) { hashmap1[s1[i] - 'a' ]++; hashmap2[s2[i] - 'a' ]++; } for (int i = windowSize; i < s2.size(); i++) { if (hashmap1 == hashmap2) return true ; hashmap2[s2[i - windowSize] - 'a' ]--; hashmap2[s2[i] - 'a' ]++; } return hashmap1 == hashmap2; } };
239.滑动窗口最大值 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
1 2 3 4 5 6 7 8 9 10 11 输入:nums = [1,3,-1,-3,5,3,6,7], k = 3 输出:[3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
1 2 输入:nums = [1], k = 1 输出:[1]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 class Solution public int [] maxSlidingWindow(int [] nums, int k) { if (nums==null ||nums.length<2 ) return nums; LinkedList<Integer> list = new LinkedList(); int [] result = new int [nums.length-k+1 ]; for (int i=0 ;i<nums.length;i++){ while (!list.isEmpty()&&nums[list.peekLast()]<=nums[i]){ list.pollLast(); } list.addLast(i); if (list.peek()<=i-k){ list.poll(); } if (i-k+1 >=0 ){ result[i-k+1 ] = nums[list.peek()]; } } return result; } }
异位词 242.有效的字母异位词 给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
1 2 输入: s = "anagram", t = "nagaram" 输出: true
1 2 输入: s = "rat", t = "car" 输出: false
1 2 3 class Solution (object) : def isAnagram (self, s, t) : return sorted(s) == sorted(t)
438.找字符串中所有的字母异位词 给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
1 2 3 4 5 输入: s = "cbaebabacd", p = "abc" 输出: [0,6] 解释: 起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。 起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。
1 2 3 4 5 6 输入: s = "abab", p = "ab" 输出: [0,1,2] 解释: 起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。 起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。 起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution {public : vector <int > findAnagrams(string s, string p) { if (s.size()<p.size()) return {}; int l = 0 , r = -1 ; vector <int > freq_s(26 , 0 ), freq_p(26 , 0 ), res; for ( int i = 0 ; i < p.size() ; i++ ){ freq_p[p[i] - 'a' ]++; freq_s[s[++r] - 'a' ]++; } if ( freq_s == freq_p ) res.push_back( l ); while ( r < s.size()-1 ){ freq_s[s[++r] - 'a' ]++; freq_s[s[l++] - 'a' ]--; if ( freq_s == freq_p ) res.push_back( l ); } return res; } };
旋转词 796.旋转字符串 给定两个字符串, A 和 B。
1 2 3 4 5 6 7 示例 1: 输入: A = 'abcde', B = 'cdeab' 输出: true 示例 2: 输入: A = 'abcde', B = 'abced' 输出: false
1 2 3 4 5 class Solution public boolean rotateString (String A, String B) return A.length() == B.length() && (A + A).contains(B); } }
58.最后一个单词的长度 给你一个字符串 s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中最后一个单词的长度。
1 2 3 4 5 6 7 8 输入:s = "Hello World" 输出:5 输入:s = " fly me to the moon " 输出:4 输入:s = "luffy is still joyboy" 输出:6
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution public int lengthOfLastWord (String s) int length = 0 ; for (int i = s.length() - 1 ; i >= 0 ; i--) { if (s.charAt(i) != ' ' ) { length++; } else if (length != 0 ) { return length; } } return length; } }
逆序 344.反转字符串 编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。
1 2 3 4 5 6 输入:s = ["h","e","l","l","o"] 输出:["o","l","l","e","h"] 输入:s = ["H","a","n","n","a","h"] 输出:["h","a","n","n","a","H"]
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution void swap (char [] s, int i, int j) s[i] ^= s[j]; s[j] ^= s[i]; s[i] ^= s[j]; } void reverseString (char [] s) for (int i = 0 , j = s.length - 1 ; i < s.length/2 ; i++, j--) { swap(s, i,j); } } }
541.反转字符串2 给定一个字符串 s 和一个整数 k,从字符串开头算起,每计数至 2k 个字符,就反转这 2k 字符中的前 k 个字符。
1 2 3 4 5 输入:s = "abcdefg", k = 2 输出:"bacdfeg" 输入:s = "abcd", k = 2 输出:"bacd"
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution public String reverseStr (String s, int k) StringBuffer res = new StringBuffer(); int length = s.length(); int start = 0 ; while (start < length) { StringBuffer temp = new StringBuffer(); int firstK = (start + k > length) ? length : start + k; int secondK = (start + (2 * k) > length) ? length : start + (2 * k); temp.append(s.substring(start, firstK)); res.append(temp.reverse()); if (firstK < secondK) { res.append(s.substring(firstK, secondK)); } start += (2 * k); } return res.toString(); } }
动态规划问题 最长公共子串 14.最长公共前缀 编写一个函数来查找字符串数组中的最长公共前缀。
1 2 3 4 5 6 7 输入:strs = ["flower","flow","flight"] 输出:"fl" 输入:strs = ["dog","racecar","car"] 输出:"" 解释:输入不存在公共前缀。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution public String longestCommonPrefix (String[] strs) if (strs.length==0 )return "" ; String s=strs[0 ]; for (String string : strs) { while (!string.startsWith(s)){ if (s.length()==0 )return "" ; s=s.substring(0 ,s.length()-1 ); } } return s; } }
最长公共子序列LCS 1143.最长公共子序列 给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
例如,”ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
1 2 3 4 5 6 7 8 9 10 11 12 输入:text1 = "abcde", text2 = "ace" 输出:3 解释:最长公共子序列是 "ace" ,它的长度为 3 。 输入:text1 = "abc", text2 = "abc" 输出:3 解释:最长公共子序列是 "abc" ,它的长度为 3 。 输入:text1 = "abc", text2 = "def" 输出:0 解释:两个字符串没有公共子序列,返回 0 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution public int longestCommonSubsequence (String text1, String text2) int m = text1.length(), n = text2.length(); int [][] dp = new int [m + 1 ][n + 1 ]; for (int i = 1 ; i <= m; i++) { for (int j = 1 ; j <= n; j++) { if (text1.charAt(i - 1 ) == text2.charAt(j - 1 )) { dp[i][j] = dp[i - 1 ][j - 1 ] + 1 ; } dp[i][j] = Math.max(dp[i - 1 ][j], dp[i][j]); dp[i][j] = Math.max(dp[i][j - 1 ], dp[i][j]); } } return dp[m][n]; } }
最长上升子序列 300. 最长递增子序列 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
1 2 3 输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
1 2 输入:nums = [0,1,0,3,2,3] 输出:4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution {public : int lengthOfLIS (vector <int >& nums) if (nums.size() <= 1 ) return nums.size(); vector <int > dp(nums.size(), 1 ); int result = 0 ; for (int i = 1 ; i < nums.size(); i++) { for (int j = 0 ; j < i; j++) { if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1 ); } if (dp[i] > result) result = dp[i]; } return result; } };
673.最长递增子序列的个数 给定一个未排序的整数数组,找到最长递增子序列的个数。
1 2 3 输入: [1,3,5,4,7] 输出: 2 解释: 有两个最长递增子序列,分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。
1 2 3 输入: [2,2,2,2,2] 输出: 5 解释: 最长递增子序列的长度是1,并且存在5个子序列的长度为1,因此输出5。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution public int findNumberOfLIS (int [] nums) if (nums.length == 0 ) { return 0 ; } int [] dp = new int [nums.length]; int [] combination = new int [nums.length]; Arrays.fill(dp, 1 ); Arrays.fill(combination, 1 ); int max = 1 , res = 0 ; for (int i = 1 ; i < dp.length; i++) { for (int j = 0 ; j < i; j++) { if (nums[i] > nums[j]) { if (dp[j] + 1 > dp[i]) { dp[i] = dp[j] + 1 ; combination[i] = combination[j]; } else if (dp[j] + 1 == dp[i]) { combination[i] += combination[j]; } } } max = Math.max(max, dp[i]); } for (int i = 0 ; i < nums.length; i++) if (dp[i] == max) res += combination[i]; return res; } }
674. 最长连续递增序列 给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。l <= i < r,都有nums[i] < nums[i + 1],那么子序列[nums[l], nums[l + 1], ..., nums[r - 1], nums[r]]就是连续递增子序列。
1 2 3 4 输入:nums = [1,3,5,4,7] 输出:3 解释:最长连续递增序列是 [1,3,5], 长度为3。 尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
1 2 3 输入:nums = [2,2,2,2,2] 输出:1 解释:最长连续递增序列是 [2], 长度为1。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution {public : int findLengthOfLCIS (vector <int >& nums) if (nums.size() == 0 ) return 0 ; int result = 1 ; vector <int > dp(nums.size() ,1 ); for (int i = 0 ; i < nums.size() - 1 ; i++) { if (nums[i + 1 ] > nums[i]) { dp[i + 1 ] = dp[i] + 1 ; } if (dp[i + 1 ] > result) result = dp[i + 1 ]; } return result; } };
括号匹配问题 22. 括号生成 数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且有效的括号组合。
示例 1
1 2 输入:n = 3 输出:["((()))","(()())","(())()","()(())","()()()"]
示例 2
每新增一对括号,就是在上一次的结果的各个位置插入一个”()”,用集合防止重复
1 2 3 4 5 6 7 8 9 10 class Solution (object) : def generateParenthesis (self, n) : result = {'' } for i in range(n): temp = set() for s in result: for j in range(len(s) + 1 ): temp.add(s[:j] + '()' + s[j:]) result = temp return list(result)
32. 最长有效括号 给你一个只包含 ‘(‘ 和 ‘)’ 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
1 2 3 输入:s = "(()" 输出:2 解释:最长有效括号子串是 "()"
1 2 3 输入:s = ")()())" 输出:4 解释:最长有效括号子串是 "()()"
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution (object) : def longestValidParentheses (self, s) : length = len(s) if length == 0 : return 0 dp = [0 ] * length for i in range(1 ,length): if s[i] == ')' : pre = i - dp[i-1 ] -1 ; if pre>=0 and s[pre] == '(' : dp[i] = dp[i-1 ] + 2 if pre>0 : dp[i] += dp[pre-1 ] return max(dp);
总结
贪心与动态规划 动态规划 动态规划处理步骤 1 2 3 4 5 6 7 # 初始化 base case dp[0][0][...] = base # 进行状态转移 for 状态1 in 状态1的所有取值: for 状态2 in 状态2的所有取值: for ... dp[状态1][状态2][...] = 求最值(选择1,选择2...)
那么既然知道了这是个动态规划问题,就要思考如何列出正确的状态转移方程?
1、确定 base case,这个很简单,显然目标金额 amount 为 0 时算法返回 0,因为不需要任何硬币就已经凑出目标金额了。
2、确定「状态」,也就是原问题和子问题中会变化的变量。由于硬币数量无限,硬币的面额也是题目给定的,只有目标金额会不断地向 base case 靠近,所以唯一的「状态」就是目标金额 amount。
3、确定「选择」,也就是导致「状态」产生变化的行为。目标金额为什么变化呢,因为你在选择硬币,你每选择一枚硬币,就相当于减少了目标金额。所以说所有硬币的面值,就是你的「选择」。
4、明确 dp 函数/数组的定义。我们这里讲的是自顶向下的解法,所以会有一个递归的 dp 函数,一般来说函数的参数就是状态转移中会变化的量,也就是上面说到的「状态」;函数的返回值就是题目要求我们计算的量。就本题来说,状态只有一个,即「目标金额」,题目要求我们计算凑出目标金额所需的最少硬币数量。所以我们可以这样定义 dp 函数:
重点在状态转移方程
斐波那契数列原暴力递归
1 2 3 4 int fib (int N) if (N == 1 || N == 2 ) return 1 ; return fib(N - 1 ) + fib(N - 2 ); }
dp 数组的迭代解法
1 2 3 4 5 6 7 8 9 10 11 12 int fib (int N) if (N == 0 ) return 0 ; int [] dp = new int [N + 1 ]; dp[0 ] = 0 ; dp[1 ] = 1 ; for (int i = 2 ; i <= N; i++) { dp[i] = dp[i - 1 ] + dp[i - 2 ]; } return dp[N]; }
凑零钱问题
给你 k 种面值的硬币,面值分别为 c1, c2 ... ck,每种硬币的数量无限,再给一个总金额 amount,问你最少需要几枚硬币凑出这个金额,如果不可能凑出,算法返回 -1
找零钱问题:通熟易懂,特别是从暴力法到带备忘录的递归,顿时明白了动态规划的核心了。其实暴力法,相当于我们心中有一颗多叉树(或者是一个图),这个二叉树恰好能够用来解决这个问题,而且找零钱问题类似于是在求解多叉树的深度。
特别是下面的代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 int coinChange (int [] coins, int amount) return dp(coins, amount) } int dp (int [] coins, int n) for (int coin : coins) { res = min(res, 1 + dp(n - coin)) } return res }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 int coinChange (int [] coins, int amount) return dp(coins, amount) } int dp (int [] coins, int amount) if (amount == 0 ) return 0 ; if (amount < 0 ) return -1 ; int res = Integer.MAX_VALUE; for (int coin : coins) { int subProblem = dp(coins, amount - coin); if (subProblem == -1 ) continue ; res = Math.min(res, subProblem + 1 ); } return res == Integer.MAX_VALUE ? -1 : res; }
那么动态规划解法(带备忘录的递归),就是利用空间(数组)来记录一些这棵树已经遍历过的结点。
通过下面的代码
dp 数组的定义:当目标金额为 i 时,至少需要 dp[i] 枚硬币凑出。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 int coinChange (int [] coins, int amount) int [] dp = new int [amount + 1 ]; Arrays.fill(dp, amount + 1 ); dp[0 ] = 0 ; for (int i = 0 ; i < dp.length; i++) { for (int coin : coins) { if (i - coin < 0 ) { continue ; } dp[i] = Math.min(dp[i], 1 + dp[i - coin]); } } return (dp[amount] == amount + 1 ) ? -1 : dp[amount]; }
118. 杨辉三角 给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
示例 1
1 2 输入: numRows = 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 21 2 输入: numRows = 1 输出: [[1]]
1 2 3 4 5 6 7 8 9 10 class Solution (object) : def generate (self, numRows) : ans = [[1 ]] for i in range(1 , numRows): lst = [0 for _ in range(i+1 )] lst[0 ], lst[-1 ] = 1 , 1 for j in range(1 ,i): lst[j] = ans[i-1 ][j-1 ] + ans[i-1 ][j] ans.append(lst) return ans
62.不同路径 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
1 2 3 4 5 6 7 输入:m = 3, n = 2 输出:3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution public int uniquePaths (int m, int n) int [][] dp = new int [m][n]; for (int i = 0 ; i < m; i++) { for (int j = 0 ; j < n; j++) { if (i == 0 || j == 0 ) dp[i][j] = 1 ; else { dp[i][j] = dp[i - 1 ][j] + dp[i][j - 1 ]; } } } return dp[m - 1 ][n - 1 ]; } }
63.不同路径2 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
网格中的障碍物和空位置分别用 1 和 0 来表示。
1 2 3 4 5 6 7 输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]] 输出:2 解释: 3x3 网格的正中间有一个障碍物。 从左上角到右下角一共有 2 条不同的路径: 1. 向右 -> 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 -> 向右
1 2 输入:obstacleGrid = [[0,1],[0,0]] 输出:1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution {public : int uniquePathsWithObstacles (vector <vector <int >>& obstacleGrid) int m = obstacleGrid.size(); int n = obstacleGrid[0 ].size(); vector <vector <int >> dp(m, vector <int >(n, 0 )); for (int i = 0 ; i < m && obstacleGrid[i][0 ] == 0 ; i++) dp[i][0 ] = 1 ; for (int j = 0 ; j < n && obstacleGrid[0 ][j] == 0 ; j++) dp[0 ][j] = 1 ; for (int i = 1 ; i < m; i++) { for (int j = 1 ; j < n; j++) { if (obstacleGrid[i][j] == 1 ) continue ; dp[i][j] = dp[i - 1 ][j] + dp[i][j - 1 ]; } } return dp[m - 1 ][n - 1 ]; } };
64. 最小路径和 给定一个包含非负整数的m x n网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
1 2 3 输入:grid = [[1,3,1],[1,5,1],[4,2,1]] 输出:7 解释:因为路径 1→3→1→1→1 的总和最小。
1 2 输入:grid = [[1,2,3],[4,5,6]] 输出:12
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution public int minPathSum (int [][] grid) int m = grid.length; int n = grid[0 ].length; int result = 0 ; int [][] dp = new int [m][n]; for (int i = 0 ; i < m; i++){ for (int j = 0 ; j < n; j++){ int cur = grid[i][j]; if (i == 0 && j == 0 ){ dp[i][j] = cur; } else if (i == 0 ){ dp[i][j] = dp[i][j-1 ] + cur; } else if (j == 0 ){ dp[i][j] = dp[i-1 ][j] + cur; } else { dp[i][j] = Math.min(dp[i-1 ][j] + cur, dp[i][j-1 ]+cur); } } } return dp[m-1 ][n-1 ]; } }
647. 回文子串 给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
1 2 3 输入:s = "abc" 输出:3 解释:三个回文子串: "a", "b", "c"
1 2 3 输入:s = "aaa" 输出:6 解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution public int countSubstrings (String s) int res = 0 ; int n = s.length(); boolean [][] dp = new boolean [n][n]; for (int i=n-1 ; i>=0 ; i--){ for (int j=i; j<n; j++){ if (s.charAt(i)==s.charAt(j) && (j-i<=2 || dp[i+1 ][j-1 ])){ dp[i][j] = true ; res++; } } } return res; } }
5. 最长回文子串 给你一个字符串 s,找到 s 中最长的回文子串。
1 2 3 输入:s = "babad" 输出:"bab" 解释:"aba" 同样是符合题意的答案。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution {public : string longestPalindrome (string s) vector <vector <int >> dp(s.size(), vector <int >(s.size(), 0 )); int maxlenth = 0 ; int left = 0 ; int right = 0 ; for (int i = s.size() - 1 ; i >= 0 ; i--) { for (int j = i; j < s.size(); j++) { if (s[i] == s[j] && (j - i <= 1 || dp[i + 1 ][j - 1 ])) { dp[i][j] = true ; } if (dp[i][j] && j - i + 1 > maxlenth) { maxlenth = j - i + 1 ; left = i; right = j; } } } return s.substr(left, maxlenth); } };
53. 最大子数组和 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
1 2 3 输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
1 2 输入:nums = [5,4,-1,7,8] 输出:23
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution public static int maxSubArray (int [] nums) if (nums.length == 0 ) { return 0 ; } int res = nums[0 ]; int [] dp = new int [nums.length]; dp[0 ] = nums[0 ]; for (int i = 1 ; i < nums.length; i++) { dp[i] = Math.max(dp[i - 1 ] + nums[i], nums[i]); res = res > dp[i] ? res : dp[i]; } return res; } }
70.爬楼梯 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
1 2 3 4 5 输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
1 2 3 4 5 6 输入:n = 3 输出:3 解释:有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution {public : int climbStairs (int n) if (n == 1 ){return 1 ;} if (n == 2 ){return 2 ;} int a = 1 , b = 2 , temp; for (int i = 3 ; i <= n; i++){ temp = a; a = b; b = temp + b; } return b; } };
121.买卖股票最佳时机 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
1 2 3 4 输入:[7,1,5,3,6,4] 输出:5 解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。 注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
1 2 3 输入:prices = [7,6,4,3,1] 输出:0 解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
思路还是挺清晰的,还是DP思想:
记录【今天之前买入的最小值】
计算【今天之前最小值买入,今天卖出的获利】,也即【今天卖出的最大获利】
比较【每天的最大获利】,取最大值即可
1 2 3 4 5 6 7 8 9 10 11 12 class Solution { public int maxProfit (int [] prices) if (prices.length <= 1 ) return 0 ; int min = prices[0 ], max = 0 ; for (int i = 1 ; i < prices.length; i++) { max = Math.max(max, prices[i] - min); min = Math.min(min, prices[i]); } return max; } }
122.买卖股票最佳时机2 给定一个数组 prices ,其中 prices[i] 是一支给定股票第 i 天的价格。
1 2 3 4 输入: prices = [7,1,5,3,6,4] 输出: 7 解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。 随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
1 2 3 4 输入: prices = [1,2,3,4,5] 输出: 4 解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。 注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
1 2 3 输入: prices = [7,6,4,3,1] 输出: 0 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
dp[i][0]第i天的状态是没买股票(两种情况:昨天没买,今天还是没买或者昨天是买了股票的状态,几天前买的我们不管,然后今天卖出去了)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution public int maxProfit (int [] prices) if (prices.length<1 ){ return prices.length; } int [][] dp = new int [prices.length][2 ]; dp[0 ][0 ] = 0 ; dp[0 ][1 ] = -prices[0 ]; for (int i=1 ;i<prices.length;i++){ dp[i][0 ] = Math.max(dp[i-1 ][1 ]+prices[i],dp[i-1 ][0 ]); dp[i][1 ] = Math.max(dp[i][0 ]-prices[i],dp[i-1 ][1 ]); } return Math.max(dp[prices.length-1 ][0 ],dp[prices.length-1 ][1 ]); } }
123.买卖股票最佳时机3 给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
1 2 3 4 输入:prices = [3,3,5,0,0,3,1,4] 输出:6 解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。 随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
1 2 3 4 5 输入:prices = [1,2,3,4,5] 输出:4 解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。 注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。 因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
1 2 3 输入:prices = [7,6,4,3,1] 输出:0 解释:在这个情况下, 没有交易完成, 所以最大利润为 0。
暴力递归,会超时,写在这里是为了让大家更好的理解动态规划的代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public int maxProfit (int [] prices) return f(prices, 0 , 0 , 0 ); } private int f (int [] prices, int i, int hasStock, int counts) if (i >= prices.length || (counts >= 2 && hasStock < 1 )) return 0 ; if (hasStock > 0 ) return Math.max(prices[i] + f(prices, i+1 , 0 , counts), f(prices, i+1 , 1 , counts)); return Math.max(-prices[i] + f(prices, i+1 , 1 , counts+1 ), f(prices, i+1 , 0 , counts)); }
动态规划 时间复杂度O(n)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution public int maxProfit (int [] prices) int m = prices.length; int [][][] dp = new int [m+1 ][2 ][3 ]; for (int i = m-1 ; i >= 0 ; i--) { for (int j = 1 ; j >= 0 ; j--) { for (int k = 2 ; k >= 0 ; k--) { if (k == 2 && j == 0 ) continue ; if (j > 0 ) dp[i][j][k] = Math.max(prices[i] + dp[i+1 ][0 ][k], dp[i+1 ][1 ][k]); else dp[i][j][k] = Math.max(-prices[i] + dp[i+1 ][1 ][k+1 ], dp[i+1 ][0 ][k]); } } } return dp[0 ][0 ][0 ]; } }
188.买卖股票最佳实际4 给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
1 2 3 输入:k = 2, prices = [2,4,1] 输出:2 解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
1 2 3 4 输入:k = 2, prices = [3,2,6,5,0,3] 输出:7 解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。 随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class Solution public int maxProfit (int k, int [] prices) if (k < 1 ) return 0 ; if (k >= prices.length/2 ) return greedy(prices); int [][] t = new int [k][2 ]; for (int i = 0 ; i < k; ++i) t[i][0 ] = Integer.MIN_VALUE; for (int p : prices) { t[0 ][0 ] = Math.max(t[0 ][0 ], -p); t[0 ][1 ] = Math.max(t[0 ][1 ], t[0 ][0 ] + p); for (int i = 1 ; i < k; ++i) { t[i][0 ] = Math.max(t[i][0 ], t[i-1 ][1 ] - p); t[i][1 ] = Math.max(t[i][1 ], t[i][0 ] + p); } } return t[k-1 ][1 ]; } private int greedy (int [] prices) int max = 0 ; for (int i = 1 ; i < prices.length; ++i) { if (prices[i] > prices[i-1 ]) max += prices[i] - prices[i-1 ]; } return max; } }
198.打家劫舍 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
1 2 3 4 输入:[1,2,3,1] 输出:4 解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。 偷窃到的最高金额 = 1 + 3 = 4 。
1 2 3 4 输入:[2,7,9,3,1] 输出:12 解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。 偷窃到的最高金额 = 2 + 9 + 1 = 12 。
1 2 3 4 5 6 7 8 9 10 11 12 class Solution public int rob (int [] nums) int n = nums.length; if (n <= 1 ) return n == 0 ? 0 : nums[0 ]; int [] memo = new int [n]; memo[0 ] = nums[0 ]; memo[1 ] = Math.max(nums[0 ], nums[1 ]); for (int i = 2 ; i < n; i++) memo[i] = Math.max(memo[i - 1 ], nums[i] + memo[i - 2 ]); return memo[n - 1 ]; } }
213.打家劫舍2 你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
1 2 3 输入:nums = [2,3,2] 输出:3 解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
1 2 3 4 输入:nums = [1,2,3,1] 输出:4 解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。 偷窃到的最高金额 = 1 + 3 = 4 。
核心原则就是:第一个和最后一个不能同时抢。 所以:要么不抢第一个,要么不抢最后一个。 注意不抢第一个的时候,最后一个可抢可不抢;另一种情况同理 取两种情况中的最大值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution (object) : def rob (self, nums) : n = len(nums) if n == 0 : return 0 if n <= 2 : return max(nums) dp1 = [0 ] * n dp1[0 ] = 0 dp1[1 ] = nums[1 ] for i in range(2 , n): dp1[i] = max(dp1[i-1 ],nums[i] + dp1[i-2 ]) dp2 = [0 ] * n dp2[0 ] = nums[0 ] dp2[1 ] = max(nums[0 ],nums[1 ]) for i in range(2 , n-1 ): dp2[i] = max(dp2[i-1 ],nums[i] + dp2[i-2 ]) return max(dp1[n-1 ],dp2[n-2 ])
337.打家劫舍3 在上次打劫完一条街道之后和一圈房屋后,小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为“根”。 除了“根”之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫,房屋将自动报警。
计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
1 2 3 4 5 6 7 8 9 10 输入: [3,2,3,null,3,null,1] 3 / \ 2 3 \ \ 3 1 输出: 7 解释: 小偷一晚能够盗取的最高金额 = 3 + 3 + 1 = 7.
1 2 3 4 5 6 7 8 9 10 输入: [3,4,5,1,3,null,1] 3 / \ 4 5 / \ \ 1 3 1 输出: 9 解释: 小偷一晚能够盗取的最高金额 = 4 + 5 = 9.
经过仔细分析(手动严肃脸),正确的解题思路大致是这样的:
对于一个以 node 为根节点的二叉树而言,如果尝试偷取 node 节点,那么势必不能偷取其左右子节点,然后继续尝试偷取其左右子节点的左右子节点。
如果不偷取该节点,那么只能尝试偷取其左右子节点。
比较两种方式的结果,谁大取谁。
由此得到一个递归函数(务必注意该函数的定义!!!):
1 2 //尝试对以 node 为根节点的二叉树进行偷取,返回能偷取的最大值 int tryRob(LinkedList::TreeNode* node)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution { unordered_map <TreeNode *, int > sums; public : int rob (TreeNode* root) return tryRob(root); } int tryRob (TreeNode* node) if (!node) return 0 ; if (sums.count(node)) return sums[node]; int res1 = 0 ; if (node->left) { res1 += (tryRob(node->left->left) + tryRob(node->left->right)); } if (node->right) { res1 += (tryRob(node->right->left) + tryRob(node->right->right)); } res1 += node->val; int res2 = tryRob(node->left) + tryRob(node->right); sums[node] = max(res1, res2); return sums[node]; } };
96.不同的二叉搜索树 给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
动态规划
假设n个节点存在二叉排序树的个数是G(n),令f(i)为以i为根的二叉搜索树的个数
n为根节点,当i为根节点时,其左子树节点个数为[1,2,3,…,i-1],右子树节点个数为[i+1,i+2,…n],所以当i为根节点时,其左子树节点个数为i-1个,右子树节点为n-i,即f(i) = G(i-1)*G(n-i),G(n) = G(0)*G(n-1)+G(1)*(n-2)+...+G(n-1)*G(0)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution (object) : def numTrees (self, n) : """ :type n: int :rtype: int """ dp = [0 ] * (n+1 ) dp[0 ] = 1 dp[1 ] = 1 for i in range(2 ,n+1 ): for j in range(1 ,i+1 ): dp[i] += dp[j-1 ] * dp[i-j] return dp[n]
95.不同的二叉搜索树2 给你一个整数 n ,请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按任意顺序返回答案。
1 2 输入:n = 3 输出:[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution public List<TreeNode> generateTrees (int n) if (n == 0 ) return new LinkedList<TreeNode>(); return generateTrees(1 ,n); } public List<TreeNode> generateTrees (int start,int end) List<TreeNode> res = new LinkedList<TreeNode>(); if (start > end){ res.add(null ); return res; } for (int i = start;i <= end;i++){ List<TreeNode> subLeftTree = generateTrees(start,i-1 ); List<TreeNode> subRightTree = generateTrees(i+1 ,end); for (TreeNode left : subLeftTree){ for (TreeNode right : subRightTree){ TreeNode node = new TreeNode(i); node.left = left; node.right = right; res.add(node); } } } return res; } }
124. 二叉树中的最大路径和 路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
1 2 3 输入:root = [1,2,3] 输出:6 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
1 2 3 输入:root = [-10,9,20,null,null,15,7] 输出:42 解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution private int ret = Integer.MIN_VALUE; public int maxPathSum (TreeNode root) getMax(root); return ret; } private int getMax (TreeNode r) if (r == null ) return 0 ; int left = Math.max(0 , getMax(r.left)); int right = Math.max(0 , getMax(r.right)); ret = Math.max(ret, r.val + left + right); return Math.max(left, right) + r.val; } }
22. 括号生成 数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且有效的括号组合。
示例 1
1 2 输入:n = 3 输出:["((()))","(()())","(())()","()(())","()()()"]
示例 2
每新增一对括号,就是在上一次的结果的各个位置插入一个”()”,用集合防止重复
1 2 3 4 5 6 7 8 9 10 class Solution (object) : def generateParenthesis (self, n) : result = {'' } for i in range(n): temp = set() for s in result: for j in range(len(s) + 1 ): temp.add(s[:j] + '()' + s[j:]) result = temp return list(result)
32. 最长有效括号 给你一个只包含 ‘(‘ 和 ‘)’ 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
1 2 3 输入:s = "(()" 输出:2 解释:最长有效括号子串是 "()"
1 2 3 输入:s = ")()())" 输出:4 解释:最长有效括号子串是 "()()"
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution (object) : def longestValidParentheses (self, s) : length = len(s) if length == 0 : return 0 dp = [0 ] * length for i in range(1 ,length): if s[i] == ')' : pre = i - dp[i-1 ] -1 ; if pre>=0 and s[pre] == '(' : dp[i] = dp[i-1 ] + 2 if pre>0 : dp[i] += dp[pre-1 ] return max(dp);
10. 正则表达式匹配 给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.'匹配任意单个字符'*'匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖整个字符串 s的,而不是部分字符串。
1 2 3 输入:s = "aa" p = "a" 输出:false 解释:"a" 无法匹配 "aa" 整个字符串。
1 2 3 输入:s = "aa" p = "a*" 输出:true 解释:因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
1 2 3 输入:s = "aab" p = "c*a*b" 输出:true 解释:因为 '*' 表示零个或多个,这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution public boolean isMatch (String s, String p) int m = s.length(); int n = p.length(); boolean [][] f = new boolean [m + 1 ][n + 1 ]; f[0 ][0 ] = true ; for (int i = 0 ; i <= m; ++i) { for (int j = 1 ; j <= n; ++j) { if (p.charAt(j - 1 ) == '*' ) { f[i][j] = f[i][j - 2 ]; if (matches(s, p, i, j - 1 )) { f[i][j] = f[i][j] || f[i - 1 ][j]; } } else { if (matches(s, p, i, j)) { f[i][j] = f[i - 1 ][j - 1 ]; } } } } return f[m][n]; } public boolean matches (String s, String p, int i, int j) if (i == 0 ) { return false ; } if (p.charAt(j - 1 ) == '.' ) { return true ; } return s.charAt(i - 1 ) == p.charAt(j - 1 ); } }
44. 通配符匹配 给定一个字符串 (s) 和一个字符模式 (p) ,实现一个支持'?'和'*'的通配符匹配。
1 2 '?' 可以匹配任何单个字符。 '*' 可以匹配任意字符串(包括空字符串)。
两个字符串完全匹配才算匹配成功。
说明:
s 可能为空,且只包含从 a-z 的小写字母。
p 可能为空,且只包含从 a-z 的小写字母,以及字符 ? 和 *。
1 2 3 4 5 输入: s = "aa" p = "a" 输出: false 解释: "a" 无法匹配 "aa" 整个字符串。
1 2 3 4 5 输入: s = "aa" p = "*" 输出: true 解释: '*' 可以匹配任意字符串。
动态规划的解决思路
dp[i][j]表示s到i位置,p到j位置是否匹配!
初始化
1 2 3 dp[0][0]:什么都没有,所以为true 第一行dp[0][j],换句话说,s为空,与p匹配,所以只要p开始为*才为true 第一列dp[i][0],当然全部为False
动态方程:
1 2 3 4 如果(s[i] == p[j] || p[j] == "?") && dp[i-1][j-1] ,有dp[i][j] = true 如果p[j] == "*" && (dp[i-1][j] = true || dp[i][j-1] = true) 有dp[i][j] = true dp[i-1][j],表示*代表是空字符,例如ab,ab* dp[i][j-1],表示*代表非空任何字符,例如abcd,ab*
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution public boolean isMatch2 (String s, String p) boolean [][] dp = new boolean [s.length() + 1 ][p.length() + 1 ]; dp[0 ][0 ] = true ; for (int j = 1 ; j < p.length() + 1 ; j++) { if (p.charAt(j - 1 ) == '*' ) { dp[0 ][j] = dp[0 ][j - 1 ]; } } for (int i = 1 ; i < s.length() + 1 ; i++) { for (int j = 1 ; j < p.length() + 1 ; j++) { if (s.charAt(i - 1 ) == p.charAt(j - 1 ) || p.charAt(j - 1 ) == '?' ) { dp[i][j] = dp[i - 1 ][j - 1 ]; } else if (p.charAt(j - 1 ) == '*' ) { dp[i][j] = dp[i][j - 1 ] || dp[i - 1 ][j]; } } } return dp[s.length()][p.length()]; } }
139.单词拆分 给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
1 2 3 输入: s = "leetcode", wordDict = ["leet", "code"] 输出: true 解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。
1 2 3 4 输入: s = "applepenapple", wordDict = ["apple", "pen"] 输出: true 解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。 注意,你可以重复使用字典中的单词。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution public boolean wordBreak (String s, List<String> wordDict) int s_len = s.length(); boolean [] dp = new boolean [s_len + 1 ]; dp[0 ] = true ; for (int i=1 ; i<=s_len; i++){ for (int j=0 ; j<i; j++){ if (dp[j] && wordDict.contains(s.substring(j, i))){ dp[i] = true ; break ; } } } return dp[s_len]; } }
140. 单词拆分 II 给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict,在字符串中增加空格来构建一个句子,使得句子中所有的单词都在词典中。返回所有这些可能的句子。
分隔时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。
1 2 3 4 5 6 7 8 输入: s = "catsanddog" wordDict = ["cat", "cats", "and", "sand", "dog"] 输出: [ "cats and dog", "cat sand dog" ]
1 2 3 4 5 6 7 8 9 输入: s = "pineapplepenapple" wordDict = ["apple", "pen", "applepen", "pine", "pineapple"] 输出: [ "pine apple pen apple", "pineapple pen apple", "pine applepen apple" ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution List<String> res = new ArrayList<>(); public List<String> wordBreak (String s, List<String> wordDict) dfs(s,wordDict,new ArrayList<>(),0 ); return res; } public void dfs (String s,List<String> wordDict,List<String> path,int index) if (index==s.length()){ res.add(new String(String.join(" " ,path))); return ; } for (int i=index;i<=s.length();i++){ if (wordDict.contains(s.substring(index,i))){ path.add(s.substring(index,i)); dfs(s,wordDict,path,i); path.remove(path.size()-1 ); } } } }
72. 编辑距离 给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
1 2 3 4 5 6 输入:word1 = "horse", word2 = "ros" 输出:3 解释: horse -> rorse (将 'h' 替换为 'r') rorse -> rose (删除 'r') rose -> ros (删除 'e')
问题1:如果 word1[0..i-1] 到 word2[0..j-1] 的变换需要消耗 k 步,那 word1[0..i] 到 word2[0..j] 的变换需要几步呢?
问题2:如果 word1[0..i-1] 到 word2[0..j] 的变换需要消耗 k 步,那 word1[0..i] 到 word2[0..j] 的变换需要消耗几步呢?
问题3:如果 word1[0..i] 到 word2[0..j-1] 的变换需要消耗 k 步,那 word1[0..i] 到 word2[0..j] 的变换需要消耗几步呢?
从上面三个问题来看,word1[0..i] 变换成 word2[0..j] 主要有三种手段,用哪个消耗少,就用哪个。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution {public : int minDistance (string word1, string word2) int m = word1.length(); int n = word2.length(); vector <vector <int >> cost(m+1 , vector <int >(n+1 )); for (int i = 0 ; i <= m; ++i) { cost[i][0 ] = i; } for (int j = 0 ; j <= n; ++j) { cost[0 ][j] = j; } for (int i = 1 ; i <= m; ++i) { for (int j = 1 ; j <= n; ++j) { if (word1[i-1 ] == word2[j-1 ]) { cost[i][j] = cost[i-1 ][j-1 ]; } else { cost[i][j] = 1 + min(cost[i-1 ][j-1 ], min(cost[i][j-1 ], cost[i-1 ][j])); } } } return cost[m][n]; } };
42.接雨水 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
1 2 3 输入:height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : int trap (vector <int >& height) int res = 0 ; int n = height.size(); vector <int > left(n), right(n); for (int i = 1 ; i < n; i++) { left[i] = max(left[i - 1 ], height[i - 1 ]); } for (int i = n - 2 ; i >= 0 ; i--) { right[i] = max(right[i + 1 ], height[i + 1 ]); } for (int i = 0 ; i < n; i++) { int level = min(left[i], right[i]); res += max(0 , level - height[i]); } return res; } };
1143.最长公共子序列 给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
1 2 3 输入:s = "bbbab" 输出:4 解释:一个可能的最长回文子序列为 "bbbb" 。
1 2 3 输入:s = "cbbd" 输出:2 解释:一个可能的最长回文子序列为 "bb" 。
1 2 3 4 5 dp[i][j]表示s[i..j]代表的字符串的最长回文子序列 d[i][i]=1 dp[i][j] = dp[i+1][j-1]+2 当s[i]=s[j] dp[i][j]=max(dp[i+1][j],dp[i][j-1]) 当s[i]!=s[j] 取s[i+1..j] 和s[i..j-1]中最长的 由于dp[i][j]需要dp[i+1][j]所以需要逆序枚举s的长度,而又因为j是递增的,所以在求解dp[i][j]时,dp[i][j-1]肯定已经求解过了
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution (object) : def longestPalindromeSubseq (self, s) : len_s = len(s) dp = [[0 ] * len_s for _ in range(len_s)] for i in range(len_s): dp[i][i]=1 for i in range(len_s-1 ,-1 ,-1 ): for j in range(i+1 ,len_s): if s[i]==s[j]: dp[i][j] = dp[i+1 ][j-1 ]+2 else : dp[i][j]=max(dp[i+1 ][j],dp[i][j-1 ]) return dp[0 ][-1 ]
300. 最长递增子序列 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
1 2 3 输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
1 2 输入:nums = [0,1,0,3,2,3] 输出:4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution {public : int lengthOfLIS (vector <int >& nums) if (nums.size() <= 1 ) return nums.size(); vector <int > dp(nums.size(), 1 ); int result = 0 ; for (int i = 1 ; i < nums.size(); i++) { for (int j = 0 ; j < i; j++) { if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1 ); } if (dp[i] > result) result = dp[i]; } return result; } };
673.最长递增子序列的个数 给定一个未排序的整数数组,找到最长递增子序列的个数。
1 2 3 输入: [1,3,5,4,7] 输出: 2 解释: 有两个最长递增子序列,分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。
1 2 3 输入: [2,2,2,2,2] 输出: 5 解释: 最长递增子序列的长度是1,并且存在5个子序列的长度为1,因此输出5。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution public int findNumberOfLIS (int [] nums) if (nums.length == 0 ) { return 0 ; } int [] dp = new int [nums.length]; int [] combination = new int [nums.length]; Arrays.fill(dp, 1 ); Arrays.fill(combination, 1 ); int max = 1 , res = 0 ; for (int i = 1 ; i < dp.length; i++) { for (int j = 0 ; j < i; j++) { if (nums[i] > nums[j]) { if (dp[j] + 1 > dp[i]) { dp[i] = dp[j] + 1 ; combination[i] = combination[j]; } else if (dp[j] + 1 == dp[i]) { combination[i] += combination[j]; } } } max = Math.max(max, dp[i]); } for (int i = 0 ; i < nums.length; i++) if (dp[i] == max) res += combination[i]; return res; } }
115.不同子序列 329.矩阵中最长的递增路径 贪心算法
广度优先算法 先举例一下 BFS 出现的常见场景好吧,问题的本质就是让你在一幅「图」中找到从起点 start 到终点 target 的最近距离,这个例子听起来很枯燥,但是 BFS 算法问题其实都是在干这个事儿
解题框架 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 // 计算从起点 start 到终点 target 的最近距离 int BFS(Node start, Node target) { Queue<Node> q; // 核心数据结构 Set<Node> visited; // 避免走回头路 q.offer(start); // 将起点加入队列 visited.add(start); int step = 0; // 记录扩散的步数 while (q not empty) { int sz = q.size(); /* 将当前队列中的所有节点向四周扩散 */ for (int i = 0; i < sz; i++) { Node cur = q.poll(); /* 划重点:这里判断是否到达终点 */ if (cur is target) return step; /* 将 cur 的相邻节点加入队列 */ for (Node x : cur.adj()) { if (x not in visited) { q.offer(x); visited.add(x); } } } /* 划重点:更新步数在这里 */ step++; } }
例题 102.二叉树的层序遍历 给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
1 2 输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution public List<List<Integer>> levelOrder(TreeNode root) { if (root == null ) return new ArrayList<>(); List<List<Integer>> res = new ArrayList<>(); Queue<TreeNode> queue = new LinkedList<TreeNode>(); queue.add(root); while (!queue.isEmpty()){ int count = queue.size(); List<Integer> list = new ArrayList<Integer>(); while (count > 0 ){ TreeNode node = queue.poll(); list.add(node.val); if (node.left != null ) queue.add(node.left); if (node.right != null ) queue.add(node.right); count--; } res.add(list); } return res; } }
107.二叉树的层序遍历2 给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
1 2 输入:root = [3,9,20,null,null,15,7] 输出:[[15,7],[9,20],[3]]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution public List<List<Integer>> levelOrderBottom(TreeNode root) { LinkedList<List<Integer>> result = new LinkedList<>(); if (root == null ) return result; Queue<TreeNode> queue = new LinkedList<>(); queue.add(root); while (!queue.isEmpty()) { List<Integer> oneLevel = new ArrayList<>(); int count = queue.size(); for (int i = 0 ; i < count; i++) { TreeNode node = queue.poll(); oneLevel.add(node.val); if (node.left != null ) queue.add(node.left); if (node.right != null ) queue.add(node.right); } result.addFirst(oneLevel); } return result; } }
深度优先算法 解题框架 1 2 3 4 5 6 7 8 9 10 result = [] def backtrack(路径, 选择列表): if 满足结束条件: result.add(路径) return for 选择 in 选择列表: 做选择 backtrack(路径, 选择列表) 撤销选择
1 2 3 4 5 6 7 8 for 选择 in 选择列表: # 做选择 将该选择从选择列表移除 路径.add(选择) backtrack(路径, 选择列表) # 撤销选择 路径.remove(选择) 将该选择再加入选择列表
例题 200. 岛屿数量 给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
1 2 3 4 5 6 7 输入:grid = [ ["1","1","1","1","0"], ["1","1","0","1","0"], ["1","1","0","0","0"], ["0","0","0","0","0"] ] 输出:1
1 2 3 4 5 6 7 输入:grid = [ ["1","1","0","0","0"], ["1","1","0","0","0"], ["0","0","1","0","0"], ["0","0","0","1","1"] ] 输出:3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution public int numIslands (char [][] grid) int res = 0 ; for (int i = 0 ;i<grid.length;i++){ for (int j =0 ;j<grid[0 ].length;j++){ if (grid[i][j]=='1' ){ res = res+1 ; dfs(grid,i,j); } } } return res; } public void dfs (char [][] grid,int i,int j) if (i>=grid.length||j>=grid[0 ].length||i<0 ||j<0 ){ return ; } if (grid[i][j]=='0' ||grid[i][j]=='2' ){ return ; } grid[i][j]='2' ; dfs(grid,i+1 ,j); dfs(grid,i-1 ,j); dfs(grid,i,j+1 ); dfs(grid,i,j-1 ); } }
695. 岛屿的最大面积 给你一个大小为 m x n 的二进制矩阵 grid 。
1 2 3 输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]] 输出:6 解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution public int maxAreaOfIsland (int [][] grid) int max = 0 ; for (int i = 0 ; i < grid.length; i++){ for (int j = 0 ; j < grid[0 ].length; j++){ if (grid[i][j] == 1 ){ max = Math.max (dfs(grid, i, j), max); } } } return max; } int dfs (int [][] grid, int i, int j) if (i < 0 || i >= grid.length || j < 0 || j >= grid[0 ].length || grid[i][j] == 0 ){ return 0 ; } grid[i][j] = 0 ; int count = 1 ; count += dfs(grid, i+1 , j); count += dfs(grid, i-1 , j); count += dfs(grid, i, j+1 ); count += dfs(grid, i, j-1 ); return count; } }
463. 岛屿的周长 给定一个 row x col 的二维网格地图 grid ,其中:grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域。
1 2 3 输入:grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]] 输出:16 解释:它的周长是上面图片中的 16 个黄色的边
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 public int islandPerimeter (int [][] grid) if (grid == null || grid.length == 0 ) { return 0 ; } int rsp = 0 ; for (int i = 0 ; i < grid.length; i++) { for (int j = 0 ; j < grid[i].length; j++) { if (grid[i][j] == 1 ) { rsp += 4 ; if (i > 0 && grid[i - 1 ][j] == 1 ) { rsp -= 2 ; } if (j > 0 && grid[i][j - 1 ] == 1 ) { rsp -= 2 ; } } } } return rsp; }
743. 网络延迟时间 有 n 个网络节点,标记为 1 到 n。
思路分析:
1 2 输入:times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2 输出:2
1 2 输入:times = [[1,2,1]], n = 2, k = 1 输出:1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution {public : int networkDelayTime (vector <vector <int >>& times, int N, int K) queue <int > myQue; vector <int > distToK(N + 1 , INT_MAX); vector <vector <int >> graph(N+1 ,vector <int >(N+1 ,-1 )); for (auto &time:times){ graph[time[0 ]][time[1 ]] = time[2 ]; } myQue.push(K); distToK[K] = 0 ; while (!myQue.empty()){ int front = myQue.front(); myQue.pop(); for (int target = 1 ; target <= N; ++target){ if (graph[front][target] != -1 && distToK[front] + graph[front][target] < distToK[target]){ distToK[target] = distToK[front] + graph[front][target]; myQue.push(target); } } } int maxRes = 0 ; for (int i = 1 ; i <= N; ++i){ maxRes = max(maxRes, distToK[i]); } return maxRes == INT_MAX? -1 : maxRes; } };
787. K 站中转内最便宜的航班 有 n 个城市通过一些航班连接。给你一个数组 flights ,其中flights[i] = [fromi, toi, pricei],表示该航班都从城市 fromi 开始,以价格 pricei 抵达 toi。
1 2 3 4 5 6 输入: n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]] src = 0, dst = 2, k = 1 输出: 200 解释: 城市航班图如下
从城市 0 到城市 2 在 1 站中转以内的最便宜价格是 200,如图中红色所示。
1 2 3 4 5 6 输入: n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]] src = 0, dst = 2, k = 0 输出: 500 解释: 城市航班图如下
从城市 0 到城市 2 在 0 站中转以内的最便宜价格是 500,如图中蓝色所示。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 class Solution public : int minRes = INT_MAX; int findCheapestPrice (int n, vector<vector<int >>& flights, int src, int dst, int K) vector<vector<int >> graph(n, vector<int >(n, -1 )); for (auto &flight : flights){ graph[flight[0 ]][flight[1 ]] = flight[2 ]; } vector<bool> visited (n, false ) ; visited[src] = true ; dfs(graph, visited, n, dst, K, 0 , src, 0 ); return minRes == INT_MAX ? -1 : minRes; } void dfs (vector<vector<int >> &graph, vector<bool> &visited, int n, int dst, int K, int haveCost, int nowSrc, int myK) if (nowSrc == dst){ minRes = min(minRes, haveCost); return ; } if (myK > K || haveCost >= minRes){ return ; } for (int i = 0 ; i < n; ++i){ if (!visited[i] && graph[nowSrc][i] != -1 ){ visited[i] = true ; dfs(graph, visited, n, dst, K, haveCost + graph[nowSrc][i], i, myK + 1 ); visited[i] = false ; } } } }; class Solution public : int findCheapestPrice (int n, vector<vector<int >>& flights, int src, int dst, int K) vector<vector<int >> dp(n, vector<int >(K + 2 , INT_MAX)); for (int k = 0 ; k <= K + 1 ; ++k){ dp[src][k] = 0 ; } for (int k = 1 ; k <= K + 1 ; ++k){ for (auto &flight : flights){ if (dp[flight[0 ]][k - 1 ] != INT_MAX){ dp[flight[1 ]][k] = min(dp[flight[1 ]][k], dp[flight[0 ]][k - 1 ] + flight[2 ]); } } } return dp[dst][K+1 ] == INT_MAX ? -1 : dp[dst][K+1 ]; } };
226. 翻转二叉树 给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
1 2 输入:root = [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]
1 2 输入:root = [2,1,3] 输出:[2,3,1]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 利用前序遍历 class Solution public TreeNode invertTree (TreeNode root) if (root == null ) return null ; TreeNode rightTree = root.right; root.right = invertTree(root.left); root.left = invertTree(rightTree); return root; } } 利用中序遍历 class Solution public TreeNode invertTree (TreeNode root) if (root == null ) return null ; invertTree(root.left); TreeNode rightNode= root.right; root.right = root.left; root.left = rightNode; invertTree(root.left); } } 利用后序遍历 class Solution public TreeNode invertTree (TreeNode root) if (root == null ) return null ; TreeNode leftNode = invertTree(root.left); TreeNode rightNode = invertTree(root.right); root.right = leftNode; root.left = rightNode; return root; } } 利用层次遍历 class Solution public TreeNode invertTree (TreeNode root) if (root == null ) return null ; Queue<TreeNode> queue = new LinkedList<>(); queue.offer(root); while (!queue.isEmpty()){ TreeNode node = queue.poll(); TreeNode rightTree = node.right; node.right = node.left; node.left = rightTree; if (node.left != null ){ queue.offer(node.left); } if (node.right != null ){ queue.offer(node.right); } } return root; } }
112. 路径总和 给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
1 2 3 输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 输出:true 解释:等于目标和的根节点到叶节点路径如上图所示。
1 2 3 4 5 6 输入:root = [1,2,3], targetSum = 5 输出:false 解释:树中存在两条根节点到叶子节点的路径: (1 --> 2): 和为 3 (1 --> 3): 和为 4 不存在 sum = 5 的根节点到叶子节点的路径。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution boolean ans = false ; public boolean hasPathSum (TreeNode root, int sum) if (root == null ) { return false ; } dfs(root,sum); return ans; } private void dfs (TreeNode root,int sum) if (root == null ) { return ; } if (root.left == null && root.right == null ) { if (sum == root.val) { ans = true ; } } dfs(root.left,sum - root.val); dfs(root.right,sum - root.val); } }
113. 路径总和 II 给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
1 2 输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:[[5,4,11,2],[5,8,4,5]]
1 2 输入:root = [1,2,3], targetSum = 5 输出:[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution public : vector<vector<int >> res; void dfs (TreeNode* root,vector<int > &tmp,int sum) if (!root) return ; tmp.push_back(root->val); if (root->val==sum&&(root->left==NULL&&root->right==NULL)){ res.push_back(tmp); } dfs(root->left,tmp,sum-root->val); dfs(root->right,tmp,sum-root->val); tmp.pop_back(); } vector<vector<int >> pathSum(TreeNode* root, int sum) { vector<int > tmp; dfs(root,tmp,sum); return res; } };
437. 路径总和 III 给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
1 2 3 输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 输出:3 解释:和等于 8 的路径有 3 条,如图所示。
1 2 输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:3
从竞赛题5346过来的,今天学到了叫做双重递归的操作,这种题目需要从每个节点开始进行类似的计算,所以第一个递归用来遍历这些节点,这二个递归用来处理这些节点,进行深度优先搜索。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution public : int count = 0 ; int pathSum (TreeNode* root, int sum) if (!root) return 0 ; dfs(root, sum) ; pathSum(root->left, sum) ; pathSum(root->right, sum); return count; } void dfs (TreeNode* root, int sum) if (!root) return ; if (sum - root->val == 0 ) count++; dfs(root->left, sum - root->val); dfs(root->right, sum - root->val); } };
543. 二叉树的直径 给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
注意:两结点之间的路径长度是以它们之间边的数目表示。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution int max = 0 ; public int diameterOfBinaryTree (TreeNode root) if (root == null ) { return 0 ; } dfs(root); return max; } private int dfs (TreeNode root) if (root.left == null && root.right == null ) { return 0 ; } int leftSize = root.left == null ? 0 : dfs(root.left) + 1 ; int rightSize = root.right == null ? 0 : dfs(root.right) + 1 ; max = Math.max(max, leftSize + rightSize); return Math.max(leftSize, rightSize); } }
257. 二叉树的所有路径 给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
1 2 输入:root = [1,2,3,null,5] 输出:["1->2->5","1->3"]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution public : vector<string> binaryTreePaths (TreeNode* root) { vector<string> res; if (root == nullptr) return res; binaryTreePaths(root, res, "" ); return res; } void binaryTreePaths (TreeNode * root, vector<string> & res, string path) path += to_string(root->val); if (root->left == nullptr && root->right == nullptr) { res.push_back(path); return ; } if (root->left) binaryTreePaths(root->left, res, path + "->" ); if (root->right) binaryTreePaths(root->right, res, path + "->" ); } };
110. 平衡二叉树 给定一个二叉树,判断它是否是高度平衡的二叉树。
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
1 2 输入:root = [3,9,20,null,null,15,7] 输出:true
1 2 输入:root = [1,2,2,3,3,null,null,4,4] 输出:false
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution private class ReturnNode boolean isB; int depth; public ReturnNode (int depth, boolean isB) this .isB = isB; this .depth = depth; } } public boolean isBalanced (TreeNode root) return isBST(root).isB; } public ReturnNode isBST (TreeNode root) if (root == null ){ return new ReturnNode(0 , true ); } ReturnNode left = isBST(root.left); ReturnNode right = isBST(root.right); if (left.isB == false || right.isB == false ){ return new ReturnNode(0 , false ); } if (Math.abs(left.depth - right.depth) > 1 ){ return new ReturnNode(0 , false ); } return new ReturnNode(Math.max(left.depth, right.depth) + 1 , true ); } }
树 基础遍历 二叉树基础遍历 144.二叉树前序遍历 给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
1 2 输入:root = [1,null,2,3] 输出:[1,2,3]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution {public : void traversal (TreeNode* cur, vector <int >& vec) if (cur == NULL ) return ; vec.push_back(cur->val); traversal(cur->left, vec); traversal(cur->right, vec); } vector <int > preorderTraversal(TreeNode* root) { vector <int > result; traversal(root, result); return result; } };
94.二叉树的中序遍历 给定一个二叉树的根节点 root ,返回它的 中序 遍历。
1 2 输入:root = [1,null,2,3] 输出:[1,3,2]
基于栈的中序遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution public List<Integer> inorderTraversal (TreeNode root) List<Integer> list = new ArrayList<>(); Stack<TreeNode> stack = new Stack<>(); TreeNode cur = root; while (cur != null || !stack.isEmpty()) { if (cur != null ) { stack.push(cur); cur = cur.left; } else { cur = stack.pop(); list.add(cur.val); cur = cur.right; } } return list; } }
145.二叉树的后序遍历 给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
1 2 输入:root = [1,null,2,3] 输出:[3,2,1]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution {public : void traversal (TreeNode* cur, vector <int >& vec) if (cur == NULL ) return ; traversal(cur->left, vec); traversal(cur->right, vec); vec.push_back(cur->val); } vector <int > postorderTraversal(TreeNode* root) { vector <int > result; traversal(root, result); return result; } };
总结-递归版前中后序遍历
递归-前序遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution {public : void traversal (TreeNode* cur, vector <int >& vec) if (cur == NULL ) return ; vec.push_back(cur->val); traversal(cur->left, vec); traversal(cur->right, vec); } vector <int > preorderTraversal(TreeNode* root) { vector <int > result; traversal(root, result); return result; } };
递归-中序遍历
1 2 3 4 5 6 void traversal (TreeNode* cur, vector <int >& vec) if (cur == NULL ) return ; traversal(cur->left, vec); vec.push_back(cur->val); traversal(cur->right, vec); }
递归-后序遍历
1 2 3 4 5 6 void traversal (TreeNode* cur, vector <int >& vec) if (cur == NULL ) return ; traversal(cur->left, vec); traversal(cur->right, vec); vec.push_back(cur->val); }
二叉树层次遍历 102.二叉树的层序遍历 给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
1 2 输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution public List<List<Integer>> levelOrder(TreeNode root) { if (root == null ) return new ArrayList<>(); List<List<Integer>> res = new ArrayList<>(); Queue<TreeNode> queue = new LinkedList<TreeNode>(); queue.add(root); while (!queue.isEmpty()){ int count = queue.size(); List<Integer> list = new ArrayList<Integer>(); while (count > 0 ){ TreeNode node = queue.poll(); list.add(node.val); if (node.left != null ) queue.add(node.left); if (node.right != null ) queue.add(node.right); count--; } res.add(list); } return res; } }
107.二叉树的层序遍历2 给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
1 2 输入:root = [3,9,20,null,null,15,7] 输出:[[15,7],[9,20],[3]]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution public List<List<Integer>> levelOrderBottom(TreeNode root) { LinkedList<List<Integer>> result = new LinkedList<>(); if (root == null ) return result; Queue<TreeNode> queue = new LinkedList<>(); queue.add(root); while (!queue.isEmpty()) { List<Integer> oneLevel = new ArrayList<>(); int count = queue.size(); for (int i = 0 ; i < count; i++) { TreeNode node = queue.poll(); oneLevel.add(node.val); if (node.left != null ) queue.add(node.left); if (node.right != null ) queue.add(node.right); } result.addFirst(oneLevel); } return result; } }
N叉树基础遍历 589.N叉树的前序遍历 给定一个 N 叉树,返回其节点值的 前序遍历 。
进阶:
1 2 输入:root = [1,null,3,2,4,null,5,6] 输出:[1,3,5,6,2,4]
1 2 输入:root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出:[1,2,3,6,7,11,14,4,8,12,5,9,13,10]
递归版解题思路:
参考二叉树的递归遍历方式:先遍历根节点,然后递归遍历左子树,再递归遍历右子树。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution List<Integer> res = new ArrayList<Integer>(); public List<Integer> preorder (Node root) if (root == null ) return res; res.add(root.val); for (Node child:root.children) { preorder(child); } return res; } }
590.N叉树的后序遍历 给定一个 N 叉树,返回其节点值的 后序遍历 。
N 叉树 在输入中按层序遍历进行序列化表示,每组子节点由空值 null 分隔(请参见示例)。
1 2 输入:root = [1,null,3,2,4,null,5,6] 输出:[5,6,3,2,4,1]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {public : vector <int > postorder(Node* root) { vector <int > result; postorder(root, result); return result; } void postorder (Node* root, vector <int >& result) if (root == nullptr ) return ; for (auto node : root->children) postorder(node, result); result.push_back(root->val); } }
429.N叉树的层序遍历 给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
1 2 输入:root = [1,null,3,2,4,null,5,6] 输出:[[1],[3,2,4],[5,6]]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution : def levelOrder (self, root: 'Node' ) -> List[List[int]]: res = [] def dfs (root, depth) : if not root: return if len(res) <= depth: res.append([]) res[depth].append(root.val) for ch in root.children: dfs(ch, depth+1 ) dfs(root, 0 ) return res class Solution : def levelOrder (self, root: 'Node' ) -> List[List[int]]: if not root:return [] res = [] def bfs (root) : queue = [root] while queue: nxt = [] tmp = [] for node in queue: tmp.append(node.val) for ch in node.children: nxt.append(ch) res.append(tmp) queue = nxt bfs(root) return res
二叉树深度 104. 二叉树的最大深度 给定一个二叉树,找出其最大深度。
1 2 3 4 5 6 7 8 示例: 给定二叉树 [3,9,20,null,null,15,7], 3 / \ 9 20 / \ 15 7 最大深度为3
1 2 3 4 5 class Solution public int maxDepth (TreeNode root) return root == null ? 0 : Math.max(maxDepth(root.left), maxDepth(root.right)) + 1 ; } }
111. 二叉树的最小深度 给定一个二叉树,找出其最小深度。
1 2 输入:root = [3,9,20,null,null,15,7] 输出:2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution public int minDepth (TreeNode root) if (root == null ) { return 0 ; } if (root.left == null && root.right != null ) { return 1 + minDepth(root.right); } if (root.right == null && root.left != null ) { return 1 + minDepth(root.left); } return 1 + Math.min(minDepth(root.left), minDepth(root.right)); } }
自顶向下 104.二叉树的最大深度 给定一个二叉树,找出其最大深度。
1 2 3 4 5 6 7 8 示例: 给定二叉树 [3,9,20,null,null,15,7], 3 / \ 9 20 / \ 15 7 最大深度为3
1 2 3 4 5 class Solution public int maxDepth (TreeNode root) return root == null ? 0 : Math.max(maxDepth(root.left), maxDepth(root.right)) + 1 ; } }
112. 路径总和 给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
1 2 3 输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 输出:true 解释:等于目标和的根节点到叶节点路径如上图所示。
1 2 3 4 5 6 输入:root = [1,2,3], targetSum = 5 输出:false 解释:树中存在两条根节点到叶子节点的路径: (1 --> 2): 和为 3 (1 --> 3): 和为 4 不存在 sum = 5 的根节点到叶子节点的路径。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution boolean ans = false ; public boolean hasPathSum (TreeNode root, int sum) if (root == null ) { return false ; } dfs(root,sum); return ans; } private void dfs (TreeNode root,int sum) if (root == null ) { return ; } if (root.left == null && root.right == null ) { if (sum == root.val) { ans = true ; } } dfs(root.left,sum - root.val); dfs(root.right,sum - root.val); } }
113. 路径总和 II 给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
1 2 输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:[[5,4,11,2],[5,8,4,5]]
1 2 输入:root = [1,2,3], targetSum = 5 输出:[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution public : vector<vector<int >> res; void dfs (TreeNode* root,vector<int > &tmp,int sum) if (!root) return ; tmp.push_back(root->val); if (root->val==sum&&(root->left==NULL&&root->right==NULL)){ res.push_back(tmp); } dfs(root->left,tmp,sum-root->val); dfs(root->right,tmp,sum-root->val); tmp.pop_back(); } vector<vector<int >> pathSum(TreeNode* root, int sum) { vector<int > tmp; dfs(root,tmp,sum); return res; } };
437. 路径总和 III 给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
1 2 3 输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 输出:3 解释:和等于 8 的路径有 3 条,如图所示。
1 2 输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:3
从竞赛题5346过来的,今天学到了叫做双重递归的操作,这种题目需要从每个节点开始进行类似的计算,所以第一个递归用来遍历这些节点,这二个递归用来处理这些节点,进行深度优先搜索。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution public : int count = 0 ; int pathSum (TreeNode* root, int sum) if (!root) return 0 ; dfs(root, sum) ; pathSum(root->left, sum) ; pathSum(root->right, sum); return count; } void dfs (TreeNode* root, int sum) if (!root) return ; if (sum - root->val == 0 ) count++; dfs(root->left, sum - root->val); dfs(root->right, sum - root->val); } };
257. 二叉树的所有路径 给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
1 2 输入:root = [1,2,3,null,5] 输出:["1->2->5","1->3"]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution public : vector<string> binaryTreePaths (TreeNode* root) { vector<string> res; if (root == nullptr) return res; binaryTreePaths(root, res, "" ); return res; } void binaryTreePaths (TreeNode * root, vector<string> & res, string path) path += to_string(root->val); if (root->left == nullptr && root->right == nullptr) { res.push_back(path); return ; } if (root->left) binaryTreePaths(root->left, res, path + "->" ); if (root->right) binaryTreePaths(root->right, res, path + "->" ); } };
129.求根节点到叶节点数字之和 给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
1 2 3 4 5 6 输入:root = [1,2,3] 输出:25 解释: 从根到叶子节点路径 1->2 代表数字 12 从根到叶子节点路径 1->3 代表数字 13 因此,数字总和 = 12 + 13 = 25
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution {public : int helper (TreeNode* root, int sum) if (!root) return 0 ; else if (!root->left && !root->right) return 10 *sum + root->val; return helper(root->left, 10 *sum + root->val) + helper(root->right, 10 *sum + root->val); } int sumNumbers (TreeNode* root) return helper(root, 0 ); } };
988.从叶节点开始的最小字符串 给定一颗根结点为 root 的二叉树,树中的每一个结点都有一个从 0 到 25 的值,分别代表字母 ‘a’ 到 ‘z’:值 0 代表 ‘a’,值 1 代表 ‘b’,依此类推。
找出按字典序最小的字符串,该字符串从这棵树的一个叶结点开始,到根结点结束。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 输入:[0,1,2,3,4,3,4] 输出:"dba" ``` ```java class Solution { public String smallestFromLeaf(TreeNode root) { dfs(root,new StringBuilder()); return res; } String res = null; public void dfs(TreeNode root,StringBuilder s){ if(root==null){ return; }else{ char c = (char)(root.val+'a'); s.append(c); dfs(root.left,s); dfs(root.right,s); if(root.left==null&&root.right==null){ String cur = s.reverse().toString(); s.reverse(); if(res==null || res.compareTo(cur)>0){ res = cur; } } s.deleteCharAt(s.length()-1); } } }
非自顶向下 687.最长同值路径 124.二叉树中最大的路径和 543.二叉树的直径 652.寻找重复的子树 236.二叉树的最近公共祖先 235.二叉搜索树的最近公共祖先
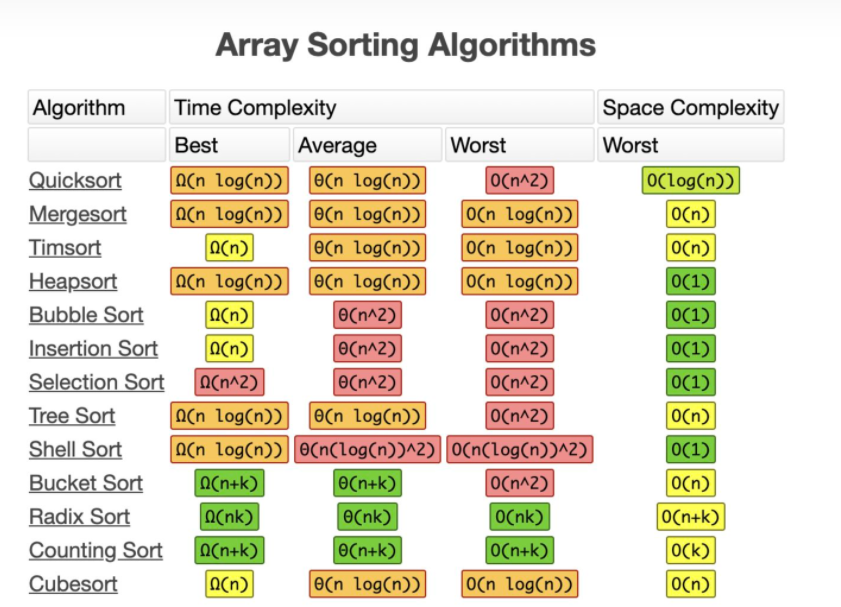




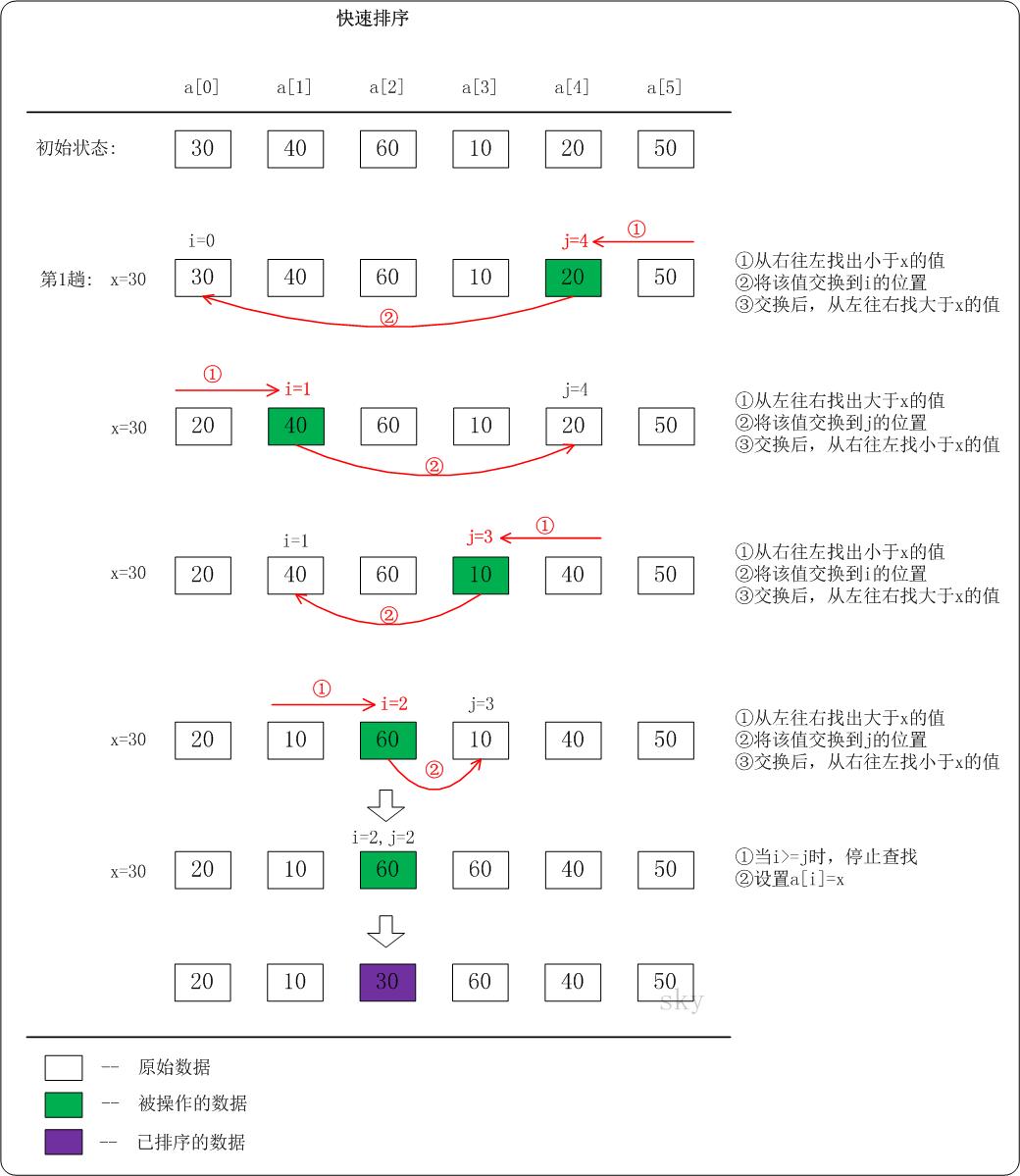


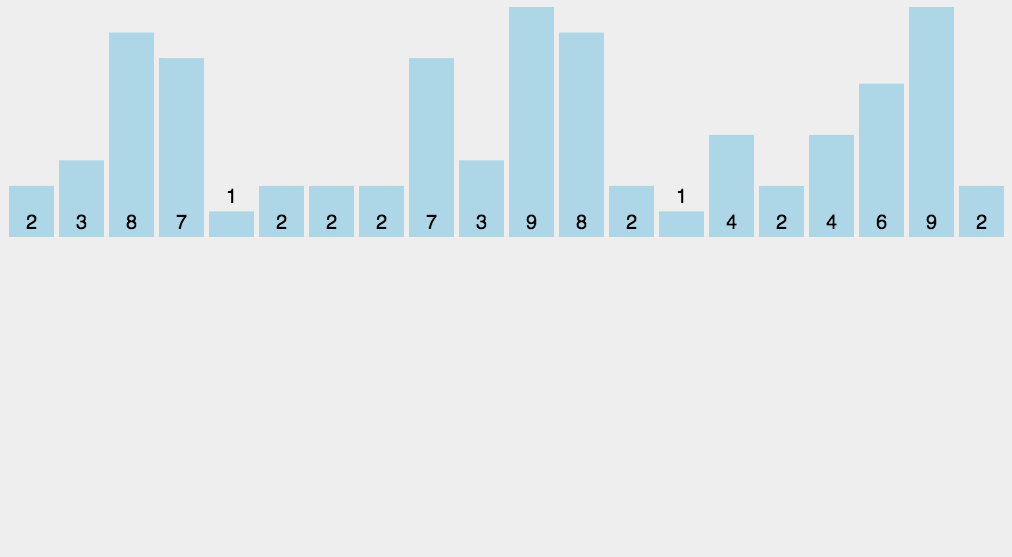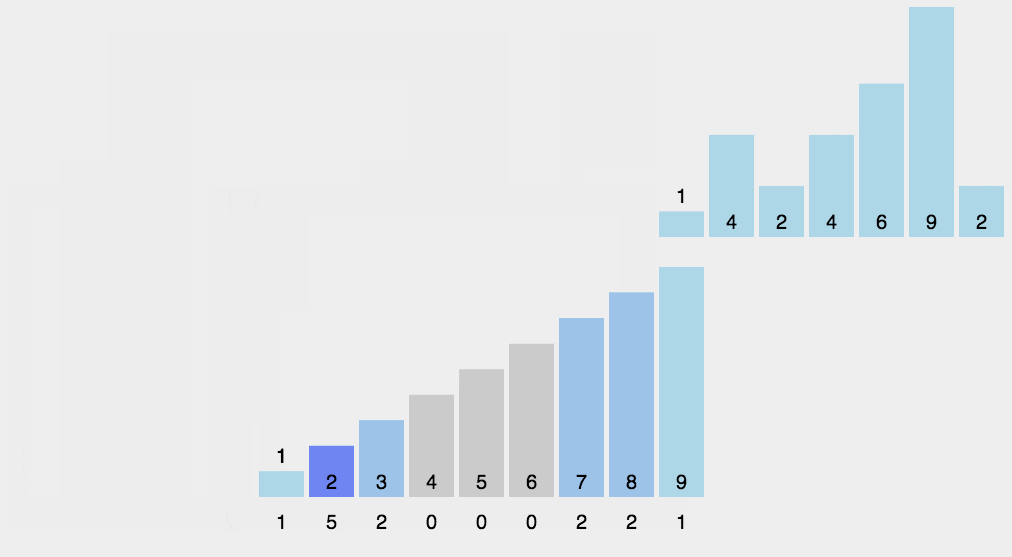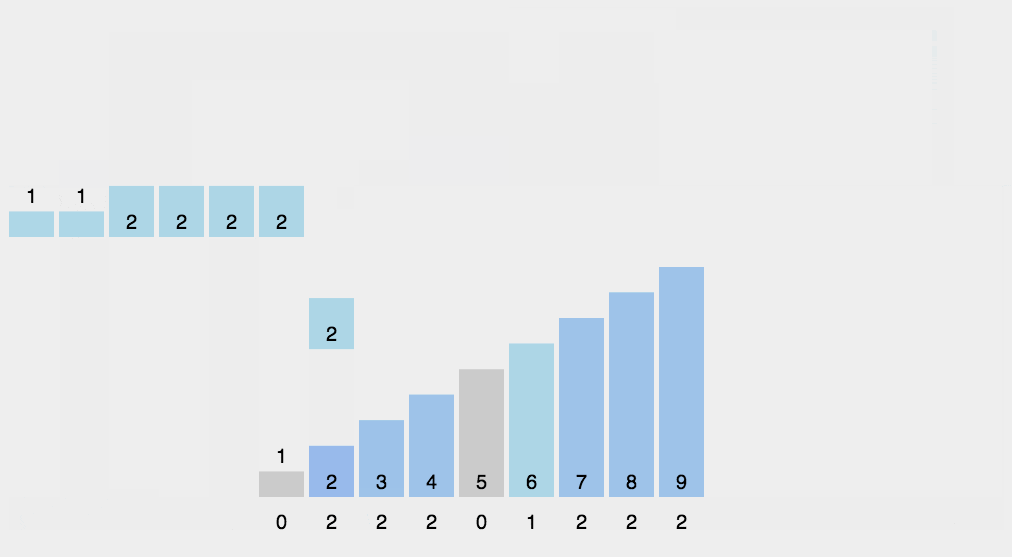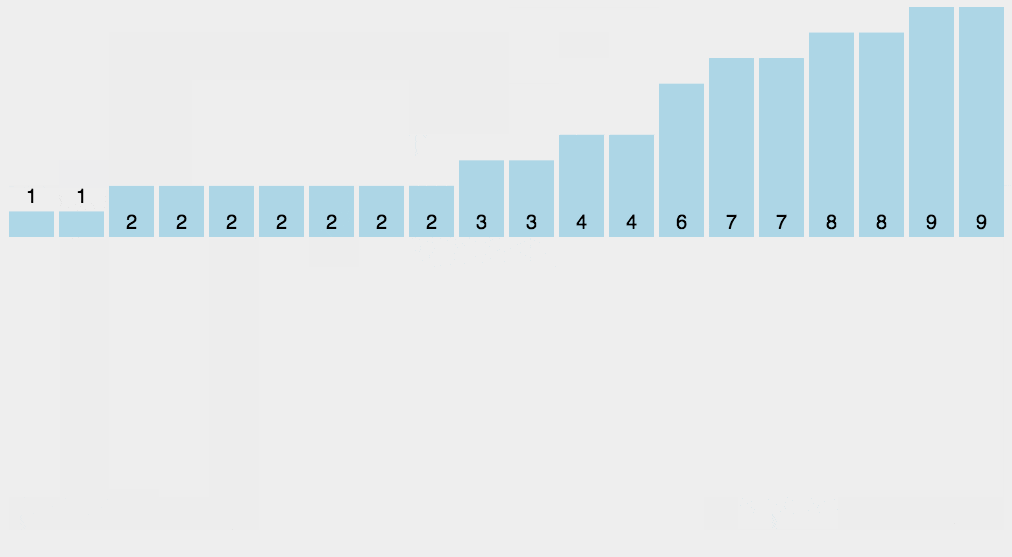
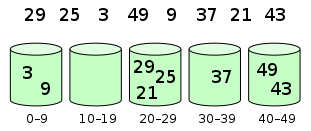

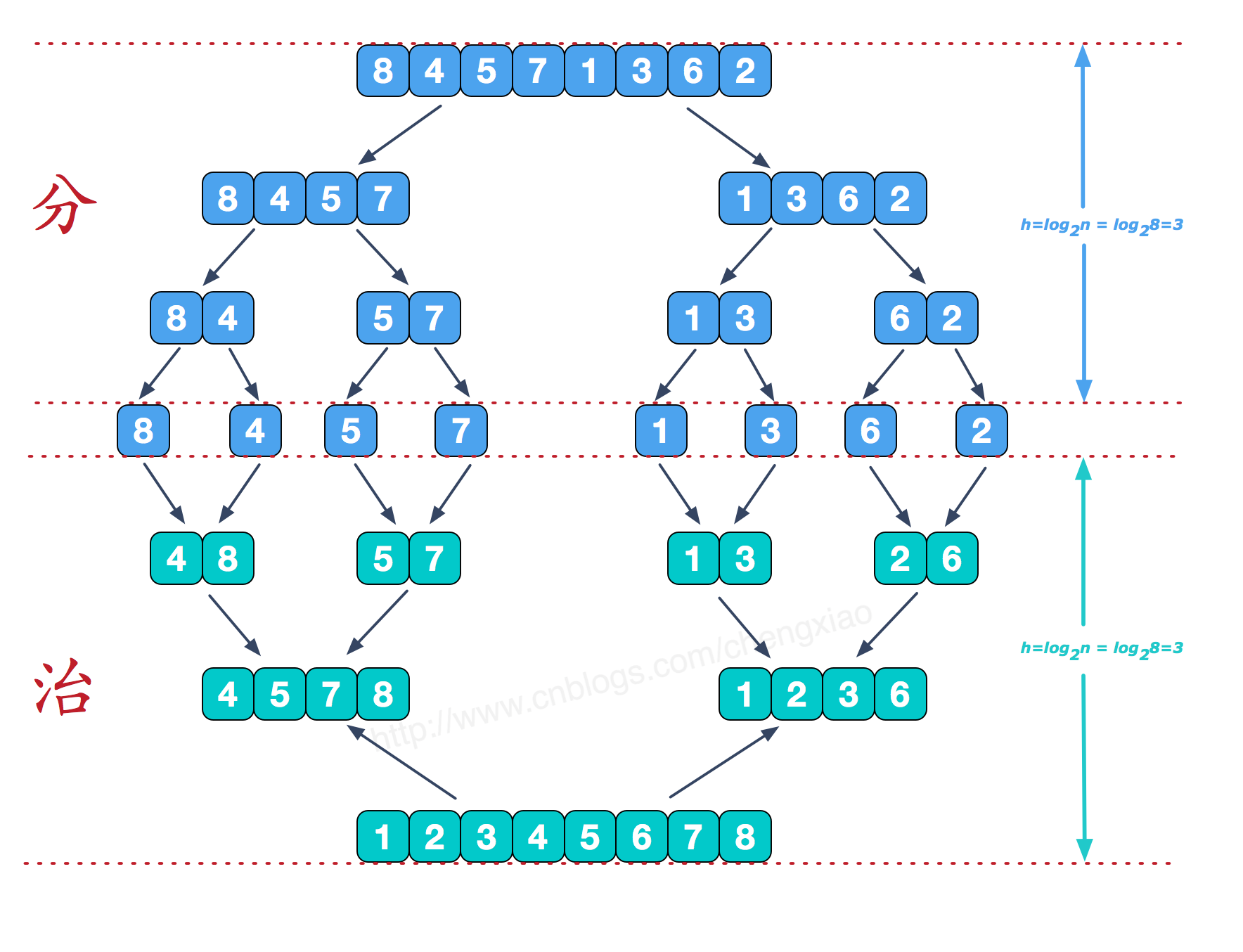




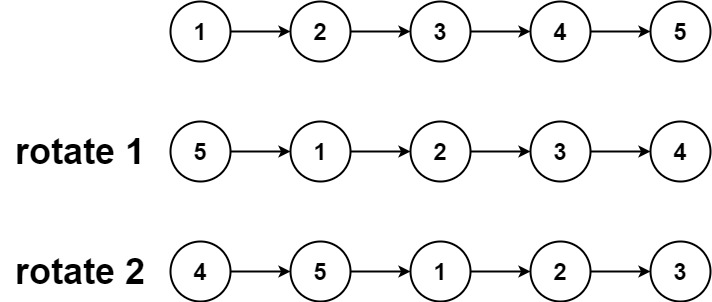

.png)

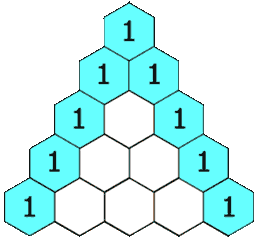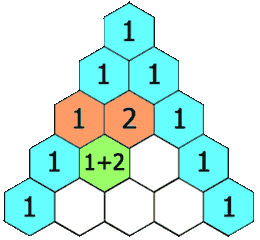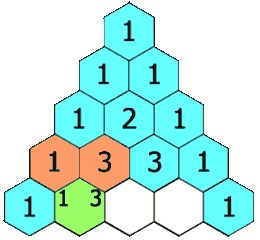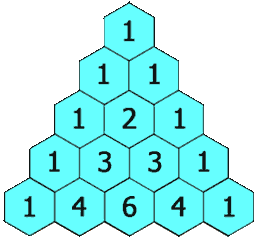





.jpg)

.jpg)



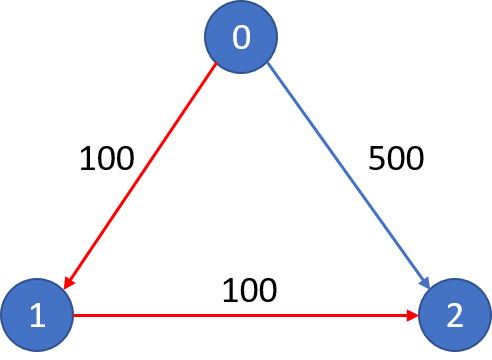
.png)
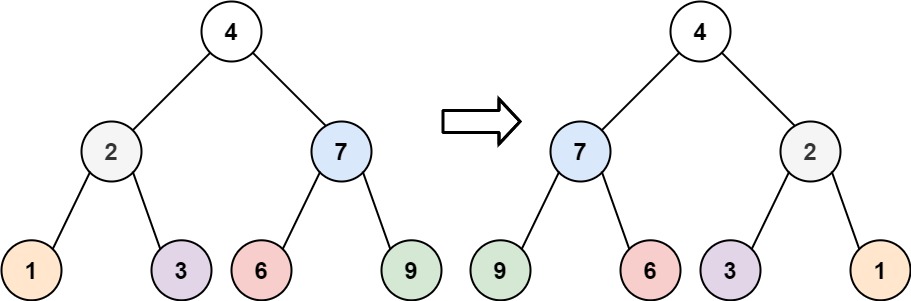
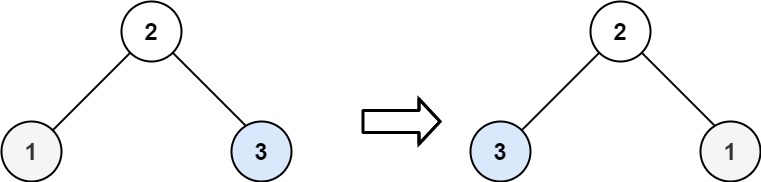

.jpg)
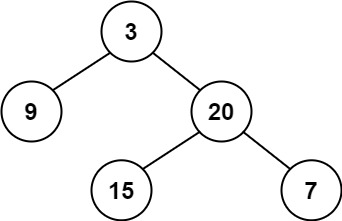
.jpg)

.jpg)



.png)
.png)
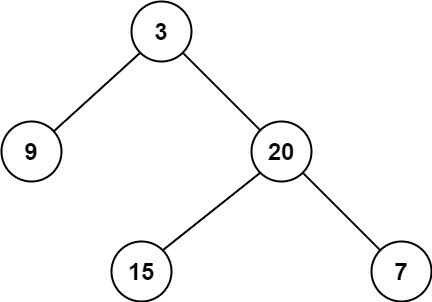



.jpg)

国内查看评论需要代理~